7．点P（t，0）是x轴上的动点，Q（0，2t）是y轴上的动点，若线段PQ与函数y=-|x|²+2|x|+3的图象只有一个公共点，则t的取值是$\frac{3}{2}$≤t＜3或t=$\frac{7}{2}$或t≤-3．

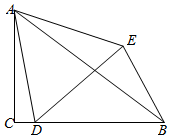6．在Rt△ACB中，∠ACB=90°，点D在边BC上，连接AD，以点D为顶点，AD为一边作等边△ADE，连接BE，若BC=7，BE=4，∠CBE=60°，则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$．

5．如图，⊙O半径为3，Rt△ABC的顶点A，B在⊙O上，∠A=30°，点C在⊙O内，当点A在圆上运动时，OC的最小值为（　　）

A．

$\sqrt{2}$

B．

$\frac{3}{2}$

C．

$\sqrt{3}$

D．

2

4．如图，在一次数学活动课上，小明用18个棱长为1的正方体积木搭成一个几何体，然后他请小亮用其他棱长为1的正方体积木在旁边再搭一个几何体，使小亮所搭几何体恰好和小明所搭几何体拼成一个无空隙的大长方体（不改变小明所搭几何体的形状）．
请从下面的A、B两题中任选一题作答，我选择A．
A、按照小明的要求搭几何体，小亮至少需要18个正方体积木．
B、按照小明的要求，小亮所搭几何体的表面积最小为46．

3．如图，作出△ABC的三条高．

2．如图，AB为⊙O的直径，$\widehat{CB}$=$\widehat{CD}$，CO的延长线交⊙O于点E，BA，ED的延长线交于点F．
（1）求证：$\widehat{AC}$=$\widehat{DE}$；
（2）若$\frac{AF}{DF}$=$\frac{2}{3}$，求$\frac{AE}{BE}$的值．

1．问题背景：在△ABC中，AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$，求此三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
（1）请你将△ABC的面积直接填写在横线上：$\frac{7}{2}$．
思维拓展：
（2）我们把上述求△ABC面积的方法叫做构图法．如果△ABC三边的长分别为$\sqrt{5}$a、$\sqrt{8}$a、$\sqrt{17}$a（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
探索创新：
（3）若△ABC三边的长分别为$\sqrt{{m}^{2}+16{n}^{2}}$、$\sqrt{9{m}^{2}+4{n}^{2}}$、$\sqrt{16{m}^{2}+4{n}^{2}}$ （m＞0，n＞0，且m≠n），试运用构图法画出示意图并求出这三角形的面积．

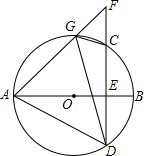20．如图，AB是⊙O直径，弦CD⊥AB于点E，G是弧AC上任意一点，延长AG，与DC的延长线相交于点F，连结AD，GD，CG，则与∠AGD相等的角有（　　）

A．

2个

B．

3个

C．

4个

D．

5个

19．已知：AD是△ABC的角平分线，DE∥AB，DF∥AC，交AB、AC分别为F，E，试判断四边形AFDE是怎样的四边形？证明你的结论．

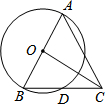18．如图，AB是⊙O的直径，BD是⊙O的弦，延长BD至点C，使得DC=BD，连接AC，OC．若AB=5，BD=$\sqrt{5}$，则OC的长为（　　）

A．

4

B．

$\frac{5}{2}$$\sqrt{3}$

C．

$\frac{9}{5}$$\sqrt{5}$

D．

$\frac{\sqrt{65}}{2}$