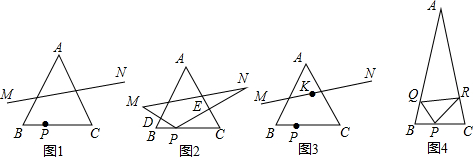
1.如图1,等边△ABC中,BC=4,点P从点B出发,沿BC方向运动到点C,点P关于直线AB、AC的对称点分别为点M、N,连接MN.
【发现】
当点P与点B重合时,线段MN的长是4$\sqrt{3}$.
当AP的长最小时,线段MN的长是6;
【探究】
如图2,设PB=x,MN
2=y,连接PM、PN,分别交AB,AC于点D,E.
(1)用含x的代数式表示PM=$\sqrt{3}$x,PN=$\sqrt{3}$(4-x);
(2)求y关于x的函数关系式,并写出y的取值范围;
(3)当点P在直线BC上的什么位置时,线段MN=3$\sqrt{7}$(直接写出答案)
【拓展】
如图3,求线段MN的中点K经过的路线长.
【应用】
如图4,在等腰△ABC中,∠BAC=30°,AB=AC,BC=2,点P、Q、R分别为边BC、AB、AC上(均不与端点重合)的动点,则△PQR周长的最小值是2+$\sqrt{3}$.
(可能用到的数值:sin75°=$\frac{\sqrt{6}+\sqrt{2}}{4}$,cos75°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,tan75°=2+$\sqrt{3}$)

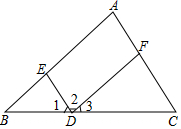 如图,填空:
如图,填空: