因式分【解析】
(x–3) (x+4) +3x=__________.

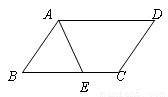
在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE＝3，若平行四边形ABCD的周长是16，则EC等于____________．

若12xm－1y2与3xyn＋1是同类项，点P（m，n）在双曲线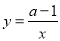上，则a的值为__________．

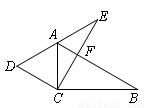
两个全等的三角尺重叠摆放在△ACB的位置，将其中一个三角尺绕着点C按逆时针方向旋转到△DCE的位置，使点A恰好落在边DE上，AB与CE相交于点F．已知∠ACB＝∠DCE＝90°，∠B＝30°，AB＝8cm，则CF＝______cm．

如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在AB边上E处，EQ与BC相交于F，若AD＝8 cm，AB＝6 cm，AE＝4cm，则△EBF的周长是______________ cm.

先化简，再求值：，从－1，2，3中选择一个适当的数作为x值代入.

如图，在Rt△ABC中，∠C=90°，∠ABC的平分线交AC于点D，点O是AB上一点，⊙O过B、D两点，且分别交AB、BC于点E、F．

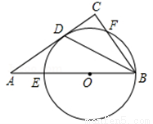
(1) 求证：AC是⊙O的切线；

(2) 已知AB=10，BC=6，求⊙O的半径r．

某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示：

（1）求a的值；

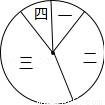
（2）若用扇形图来描述，求分数在8≤m＜9内所对应的扇形图的圆心角大小；

（3）将在第一组内的两名选手记为：A1、A2，在第四组内的两名选手记为：B1、B2，从第一组和第四组中随机选取2名选手进行调研座谈，求第一组至少有1名选手被选中的概率（用树状图或列表法列出所有可能结果）．

如图所示，某人在山坡坡脚A处测得电视塔尖点C 的仰角为60°，沿山坡向上走到P处再测得C的仰角为45°，已知OA＝200米，山坡坡度为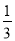（即tan∠PAB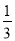＝），且O、A、B在同一条直线上，求电视塔OC的高度以及此人所在位置点P的垂直高度．（测倾器的高度忽略不计，结果保留根号）

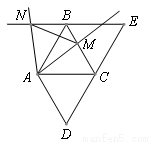
已知，如图，将∠D＝60°的菱形ABCD沿对角线AC剪开，将△ADC沿射线DC方向平移，得到△BCE. 点M为BC边上一点（点M不与点B、点C重合），将射线AM绕点A逆时针旋转60°，与EB的延长线交于点N，连接MN.

（1）求证：∠ANB＝∠AMC；

（2）探究△AMN的形状，并说明理由.