
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
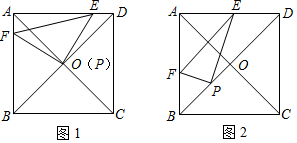
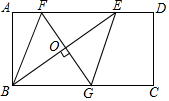 如图,在矩形ABCD中,E是AD边上一点,连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连按BF和EG,试判断四边形BFEG的形状,并说明理由.
如图,在矩形ABCD中,E是AD边上一点,连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连按BF和EG,试判断四边形BFEG的形状,并说明理由.查看答案和解析>>
科目: 来源: 题型:解答题
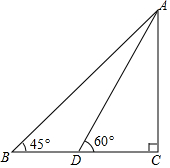 如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)
如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)查看答案和解析>>
科目: 来源: 题型:解答题
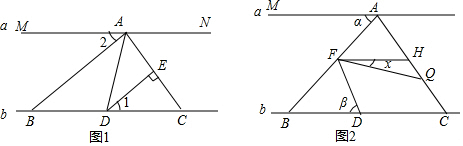
查看答案和解析>>
科目: 来源: 题型:解答题
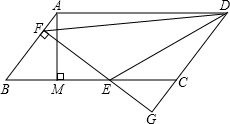 如图,?ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF.
如图,?ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com