科目： 来源： 题型：解答题

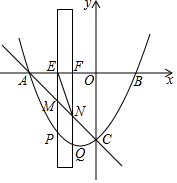16．如图，已知抛物线y=$\frac{1}{3}{x}^{2}+\frac{2}{3}$x-5与x轴交于A、B两点（点B在点A的右侧），与y轴交于点C，有一宽度为1，长度足够的矩形（阴影部分）沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和点Q，交直线AC于点M和点N，交x轴于点E和点F．
（1）求点A、B、C的坐标；
（2）当点M和点N都在线段AC上时，连接EN，如果点E的坐标为（-4，0），求sin∠ANE的值；
（3）在矩形平移过程中，当以点P、Q、N、M为顶点的四边形是平行四边形时，求点N的坐标．

科目： 来源： 题型：解答题

15．实践与操作：
      一般地，如果把一个图形绕着一个定点旋转一定角度α（α小于360°）后，能够与原来的图形重合，那么这个图形叫做旋转对称图形，这个定点叫做旋转对称中心，α叫做这个旋转对称图形的一个旋转角，请根据上述规定解答下列问题：
（1）请写出一个有一个旋转角是90°旋转对称图形，这个图形可以是正方形；
（2）尺规作图：在图中的等边三角形内部作出一个图形，使作出的图形和这个等边三角形构成的整体既是一个旋转对称图形又是一个轴对称图形（作出的图形用实线，作图过程用虚线，保留痕迹，不写做法）．

科目： 来源： 题型：填空题

科目： 来源： 题型：选择题

13．如图，AB∥CD，∠B=68°，∠E=20°，则∠D的度数为（　　）

A．

28°

B．

38°

C．

48°

D．

88°

科目： 来源： 题型：解答题

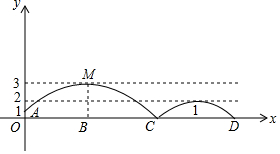12．如图，需在一面墙上绘制两个形状相同的抛物绒型图案，按照图中的直角坐标系，最高点M到横轴的距离是4米，到纵轴的距离是6米；纵轴上的点A到横轴的距离是1米，右侧抛物线的最大高度是左侧抛物线最大高度的一半．（结果保留整数或分数，参考数据：$\sqrt{3}$=$\frac{7}{4}$，$\sqrt{6}$=$\frac{5}{2}$）
（1）求左侧抛物线的表达式；
（2）求右侧抛物线的表达式；
（3）求这个图案在水平方向上的最大跨度是多少米．

科目： 来源： 题型：解答题

11．已知∠ACB=90°，AC=BC，D为平面内一点，AD⊥BD于D，连接DA，DB，DC．
（1）如图①，求证：DA+DB=$\sqrt{2}$DC；
（2）如图②，图③，线段DA．DB，DC之间又有怎样的数量关系？写出你的猜想，不需要证明；
（3）在（1），（2）的条件下，连按AB，若AB=6$\sqrt{2}$，∠DCB=30°，则CD=3$\sqrt{3}$+3．

科目： 来源： 题型：选择题

10．如图，曲线AB是顶点为B，与y轴交于点A的抛物线y=-x²+4x+2的一部分，曲线BC是双曲线y=$\frac{k}{x}$的一部分，由点C开始不断重复“A-B-C”的过程，形成一组波浪线，点P（2017，m）与Q（2025，n）均在该波浪线上，过点P、Q分别作x轴的垂线，垂足为M、N，连结PQ，则四边形PMNQ的面积为（　　）

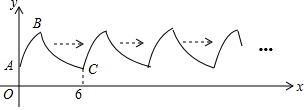
A．

72

B．

36

C．

16

D．

9

科目： 来源： 题型：选择题

9．已知圆形纸片⊙O的直径为2，将其沿着两条互相垂直的直径折叠，得到四层的扇形，将最上的一层“撑”开来，“鼓”成一个无底的圆锥，则这个圆锥的高是（　　）

A．

$\frac{1}{2}$

B．

$\frac{\sqrt{2}}{2}$

C．

$\frac{\sqrt{3}}{2}$

D．

1

科目： 来源： 题型：选择题

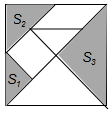8．有一副七巧板如图所示，其中三个阴影部分的面积分别为S₁，S₂，S₃，则S₁：S₂：S₃=（　　）

A．

1：2：3

B．

1：$\sqrt{2}$：2

C．

1：$\sqrt{2}$：4

D．

1：2：4

科目： 来源： 题型：解答题

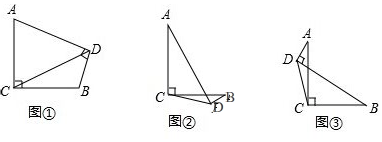
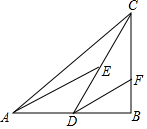7．定义：有两条边长的比值为$\frac{1}{2}$的直角三角形叫“潜力三角形”．如图，在△ABC中，∠B=90°，D是AB的中点，E是CD的中点，DF∥AE交BC于点F．
（1）设“潜力三角形”较短直角边长为a，斜边长为c，请你直接写出$\frac{c}{a}$的值为2或$\sqrt{5}$；
（2）若∠AED=∠DCB，求证：△BDF是“潜力三角形”；
（3）若△BDF是“潜力三角形”，且BF=1，求线段AC的长．