10．已知在x轴上有线段AB，且AB为2$\sqrt{3}$个单位长度，以AB为边作等边△ABC，使点C落在二次函数y=x²-2x-2的图象上，则点C的坐标为（1+$\sqrt{6}$，3）或（1-$\sqrt{6}$，3）或（1，-3）．

9．如图，在△ABC中，AB=AC=5，AB边上的高CD=4，点P从点A出发，沿AB以每秒3个单位长度的速度向终点B运动，当点P不与点A、B重合时，过点P作PQ⊥AB，交边AC或边BC于点Q，以PQ为边向右侧作正方形PQMN．设正方形PQMN与△ABC重叠部分图形的面积为S（平方单位），点P运动的时间为t（秒）．
（1）求tanB的值．
（2）求点M落在边BC上时t的值．
（3）当正方形PQMN与△ABC重叠部分为四边形时，求S与t之间的函数关系式．
（4）边BC将正方形PQMN的面积分为两部分时，设这两部分的面积比为k，当0＜k≤$\frac{1}{3}$时，直接写出t的取值范围．

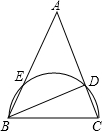8．如图，在△ABC中，AB=AC，以BC为直径画半圆交AB于E，交AC于D，$\widehat{CD}$的度数为40°，则∠A的度数是（　　）

A．

40°

B．

70°

C．

50°

D．

20°

7．如图，P为矩形ABCD边上的一个动点，沿ABCD方向运动，P点运动的路程为x．△PAD的面积为y，则y与x的函数关系用图象表示大致是（　　）

A．

B．

C．

D．

6．综合与实践：
问题情境：
    在综合实践课上，老师让同学们以“正方形纸片的剪拼”为主题展开教学活动，如图1，将一张正方形纸片ABCD沿对角线BD剪开，得到△ABD和△BCD，点O是对角线BD的中点．
操作发现：
（1）将图（1）中的△BCD沿DA方向平移，点D的对应点为D′，点B的对应点为B′，点O的对应点为O′，B′D′与AB交于点P，D′C与BD交于点Q，得到图（2），则四边形D′PBQ的形状是平行四边形．
（2）“实践小组”的同学将图（1）中的△BCD以点D为旋转中心，按顺时针方向旋转45°，得到△B′C′D，点O的对应点为O′，B′C′与AB交于点E，连接AO，O′C′交于点F，得到图（3），发现四边形AEC′F是菱形，请你证明这个结论．
实践探究：
（3）“创新小组”在实践小组操作的基础上，将图（3）中的△B′C′D以点C′为旋转中心，按逆时针方向旋转，使得C′D′⊥AD，垂足为M，B′C′⊥AB，垂足为N，分别连接OM，MO′，O′N，ON，得到图（4），他们认为四边形OMO′N是正方形．“创新小组”的发现是否正确？请你说明理由．
（4）请你参照以上操作，将图（1）中的△BCD在同一平面内进行一次图形变换，得到△B′C′D′，在图（5）中画出图形变换后构造出的新图形．标明字母，说明图形变换及构图方法，写出你发现的结论，不必证明．

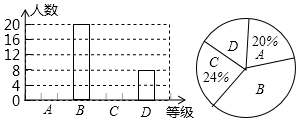5．某校九年级一次模拟考试后，数学考试为了了解学生的学习情况，在全校1000名九年级学生中，随机抽取了50名学生的数学成绩进行统计分析，并绘制了如下统计表和统计图（部分信息未给全）．

成绩/分	111～120	101～110	91～100	90及90以下
等级	A	B	C	D
学生人数	m	20	n	8

根据上面的统计图表，回答下列问题：
（1）补全条形统计图，并求出扇形统计图中，表示成绩为B等级的扇形所对的圆心角的度数；
（2）被调查学生在这次模拟考试中，数学成绩的中位数落在B等级．
（3）请估计该校九年级学生在这次模拟考试中，数学成绩在B等级以上（含B等级）的学生可达多少名？

4．如图所示，平面直角坐标系的原点O是等边△ABC的中心，A（0，1），把△ABC绕点O顺时针旋转，每秒旋转60°，则第2017秒时，点A的坐标为（　　）

A．

（0，1）

B．

（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$）

C．

（$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$）

D．

（-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$）

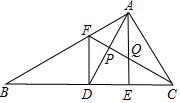3．如图，D为△ABC中边BC中点，E为CD上一点，将△ACE沿AE折叠时C与D重合，F为AB上一点，FB=FC，FC与AD、AE分别交于P、Q点，下列结论
①AE∥DF；②△APQ≌△DPF；
③AF=DF；④$\frac{AF}{CP}=\frac{2}{3}$．
其中正确的有①②④．

2．如表是某毕业班理化实验测试的分数分布，对于不同的x，下列关于分数的统计量不会发生改变的是（　　）

分数/分	7	8	9	10
频数	2	9-x	x+14	24

A．

众数、方差

B．

中位数、方差

C．

众数、中位数

D．

平均数、中位数

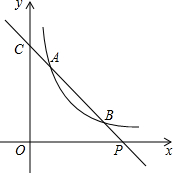1．如图，已知直线y=ax+b与双曲线y=$\frac{k}{x}$（x＞0）交于A（x₁，y₁），B（x₂，y₂）两点（A与B不重合），直线AB与x轴交于P（x₀，0），与y轴交于点C．已知A，B两点的坐标分别为（1，3），（3，y₂）．
（1）求点P的坐标；
（2）求三角形OAB的面积；
（3）在x轴上找到一点H，使HA+HB的值最小，求出符合条件的点H的坐标及HA+HB的值的最小值．