
科目: 来源: 题型:选择题
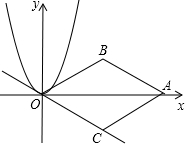 如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )
如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )| A. | $\sqrt{3}$≤m≤3$\sqrt{3}$ | B. | 3$\sqrt{3}$≤m≤$\frac{10}{3}$$\sqrt{3}$ | C. | $\frac{10}{3}$$\sqrt{3}$≤m≤$\frac{16}{3}$$\sqrt{3}$ | D. | $\sqrt{3}$≤m≤$\frac{16}{3}$$\sqrt{3}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
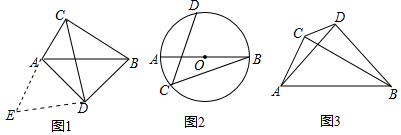
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
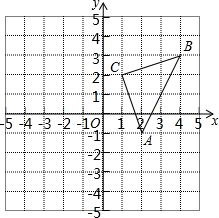 如图,直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,-1),将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,
如图,直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,-1),将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
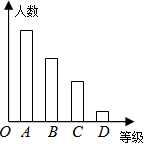 某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:
某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com