
科目: 来源: 题型:解答题
 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF查看答案和解析>>
科目: 来源: 题型:解答题
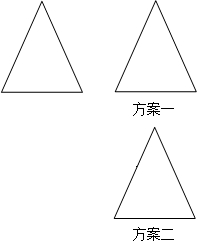 张倩同学打算制作一个平行四边形纸板,但手中只有一块等腰三角形纸板.张倩同学想了一下,用剪刀只剪了一刀,便得到一个平行四边形,且纸板充分利用没有浪费.你知道张倩是怎样剪的吗?用虚线表示出剪刀线;并请你画出两种张倩所拼的平行四边形.
张倩同学打算制作一个平行四边形纸板,但手中只有一块等腰三角形纸板.张倩同学想了一下,用剪刀只剪了一刀,便得到一个平行四边形,且纸板充分利用没有浪费.你知道张倩是怎样剪的吗?用虚线表示出剪刀线;并请你画出两种张倩所拼的平行四边形.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
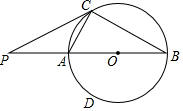 在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.
在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com