
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
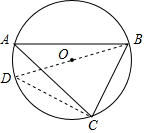 如图,⊙O是△ABC的外接圆,半径为R.已知BC=a,AC=b,AB=c.
如图,⊙O是△ABC的外接圆,半径为R.已知BC=a,AC=b,AB=c.查看答案和解析>>
科目: 来源: 题型:解答题
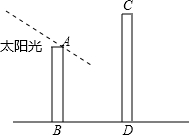 如图,AB为某一小区内的居民楼,高为18米,为缓解住房紧张的状况,现决定在这栋居民楼后面盖一栋新楼(图中CD),它的一楼是6米高的小区超市,当太阳光与水平线的夹角为30°时.
如图,AB为某一小区内的居民楼,高为18米,为缓解住房紧张的状况,现决定在这栋居民楼后面盖一栋新楼(图中CD),它的一楼是6米高的小区超市,当太阳光与水平线的夹角为30°时.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
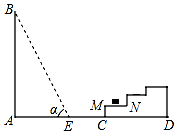 如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=34.5米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=20米,现有一只小猫睡在台阶的MN这层上晒太阳.($\sqrt{3}$取1.73)
如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=34.5米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=20米,现有一只小猫睡在台阶的MN这层上晒太阳.($\sqrt{3}$取1.73)查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
 把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )| A. | x>4,x≤1 | B. | x<4,x≥-1 | C. | x>4,x>-1 | D. | x≤4,x>-1 |
查看答案和解析>>
科目: 来源: 题型:解答题
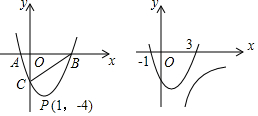
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com