科目： 来源： 题型：选择题

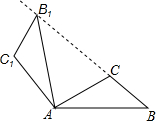15．如图，将△ABC绕点A按逆时针方向旋转100°，得到△AB₁C₁，若点B₁在线段BC的延长线上，则∠BB₁C₁的大小为（　　）

A．

70°

B．

80°

C．

84°

D．

86°

科目： 来源： 题型：解答题

14．为了解学生体育训练的情况，某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试（把测试结果分为四个等级：A级、B级、C级、D级），并就爱那个测试结果绘成了如下两幅不完整的统计图，请根据统计图中的信息解答下列问题：

（1）本次抽样测试的学生人数是400；
（2）扇形图中∠α的度数是108°，并把条形统计图补充完整；
（3）对A，B，C，D四个等级依次赋分为90，75，65，55（单位：分），比如：等级为A的同学体育得分为90分，…，依此类推．该市九年级共有学生32000名，如果全部参加这次体育测试，估计该市九年级不及格（即60分以下）学生的人数．

科目： 来源： 题型：填空题

13．如图，A、B、C是⊙O上的三点，若∠C=30°，OA=3，则弧AB的长为π．（结果保留π）

科目： 来源： 题型：选择题

12．如图，在△ABC中，AB=AC，过点A作AD∥BC，若∠1=50°，则∠CAD的大小为（　　）

A．

50°

B．

65°

C．

80°

D．

60°

科目： 来源： 题型：解答题

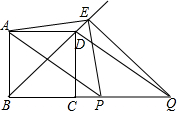11．如图，BD是正方形ABCD的对角线，BC=2，动点P从点B出发，以每秒1个单位长度的速度沿射线BC运动，同时动点Q从点C出发，以相同的速度沿射线BC运动，当点P出发后，过点Q作QE⊥BD，交直线BD于点E，连结AP、AE、PE、QE，设运动时间为t（秒）．
（1）请直接写出动点P运动过程中，四边形APQD是什么四边形？
（2）请判断AE，PE之间的数量关系和位置关系，并加以证明．
（3）设△EPB的面积为y，求y与t之间的函数关系式．
（4）直接写出△EPQ的面积是△EDQ面积的2倍时t的值．

科目： 来源： 题型：解答题

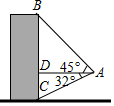10．如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为45°，测得底部C的仰角为32°，已知该建筑物高BC为208米，求此时航拍无人机与该建筑物的水平距离AD（精确到0.1米）
【参考数据：sin32°=0.5299，cos32°=0.8480，tan32°=0.6249】

科目： 来源： 题型：填空题

9．如图，以点O为圆心的半圆经过点C，AB为直径，若AC=BC=$\sqrt{2}$，则图中阴影部分的面积是$\frac{π}{4}$．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

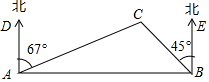7．一艘救生船在码头A接到小岛C处一艘渔船的求救信号，立即出发，沿北偏东67°方向航行10海里到达小岛C处，将人员撤离到码头A张东方向的码头B，测得小岛C位于码头B西北方向，求码头B与小岛C的距离（结果精确到0.1海里）．
【参考数据：sin23°=0.39，cos23°=0.92，tan23°=0.42，$\sqrt{2}$=1.41】

科目： 来源： 题型：解答题

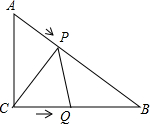6．已知：Rt△ABC中，∠ACB=90°，CA=3，CB=4，设P，Q分别为AB边，CB边上的动点，它们同时分别从A，C出发，以每秒1个单位长度的速度向终点B运动，设P，Q运动的时间为t秒．
（1）求△CPQ的面积S与运动时间t之间的函数关系式，并求出S的最大值．
（2）t为何值时，△CPQ为直角三角形．
（3）①探索：△CPQ是否可能为正三角形，说明理由．
②P，Q两点同时出发，若点P的运动速度不变，试改变点Q的运动速度，使△CPQ为正三角形，求出点Q的运动速度和此时的t值．