
科目: 来源: 题型:选择题
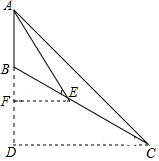 如图,测量人员计划测量山坡上一信号塔的高度,测量人员在山脚C处,测得塔顶A的仰角为45°,测量人员沿着坡度i=1:$\sqrt{3}$的山坡BC向上行走100米到达E处,再测得塔顶A的仰角为53°,则山坡的高度BD约为(精确到0.1米,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈4/3,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)( )
如图,测量人员计划测量山坡上一信号塔的高度,测量人员在山脚C处,测得塔顶A的仰角为45°,测量人员沿着坡度i=1:$\sqrt{3}$的山坡BC向上行走100米到达E处,再测得塔顶A的仰角为53°,则山坡的高度BD约为(精确到0.1米,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈4/3,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)( )| A. | 100.5米 | B. | 110.5米 | C. | 113.5米 | D. | 116.5米 |
查看答案和解析>>
科目: 来源: 题型:解答题
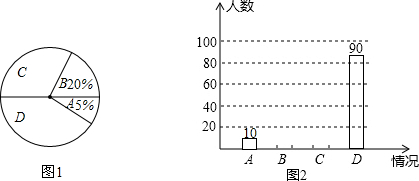
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | y=-x2-1 | B. | y=-x2-5 | C. | y=-(x-4)2-1 | D. | y=-(x-4)2-5 |
查看答案和解析>>
科目: 来源: 题型:填空题
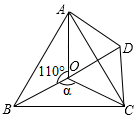 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连结OD,当α=150°时,△AOD是直角三角形.
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连结OD,当α=150°时,△AOD是直角三角形.查看答案和解析>>
科目: 来源: 题型:选择题
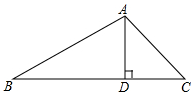 如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )| A. | 10 | B. | 10$\sqrt{2}$ | C. | 10$\sqrt{3}$ | D. | 15 |
查看答案和解析>>
科目: 来源: 题型:解答题
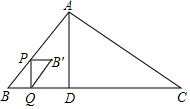 如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA-AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是$\sqrt{5}$cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA-AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是$\sqrt{5}$cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).查看答案和解析>>
科目: 来源: 题型:解答题
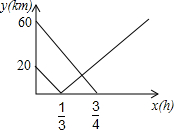 在连接A、B两市的公路之间有一个机场C,机场大巴由A市驶向机场C,货车由B市驶向A市,两车同时出发匀速行驶,图中线段、折线分别表示机场大巴、货车到机场C的路程y(km)与出发时间x(h)之间的函数关系图象.
在连接A、B两市的公路之间有一个机场C,机场大巴由A市驶向机场C,货车由B市驶向A市,两车同时出发匀速行驶,图中线段、折线分别表示机场大巴、货车到机场C的路程y(km)与出发时间x(h)之间的函数关系图象.查看答案和解析>>
科目: 来源: 题型:解答题
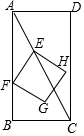 如图,在矩形ABCD中,AB=4,BC=2,点E从点A出发,以每秒$\sqrt{5}$个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
如图,在矩形ABCD中,AB=4,BC=2,点E从点A出发,以每秒$\sqrt{5}$个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com