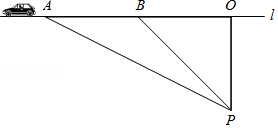6．交通安全是社会关注的热点问题，安全隐患主要是超速和超载．某中学八年级数学活动小组的同学进行了测试汽车速度的实验．如图，先在笔直的公路1旁选取一点P，在公路1上确定点O、B，使得PO⊥l，PO=100米，∠PBO=45°．这时，一辆轿车在公路1上由B向A匀速驶来，测得此车从B处行驶到A处所用的时间为3秒，并测得∠APO=60°．此路段限速每小时80千米，试判断此车是否超速？请说明理由（参考数据：$\sqrt{2}$=1.41，$\sqrt{3}$=1.73）．

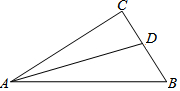5．如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，若CD=4，AC=12，AB=15，则△ABC的面积为（　　）

A．

48

B．

50

C．

54

D．

60

4．计算（-xy²）³的结果是（　　）

A．

x3y6

B．

-x3y6

C．

-x4y5

D．

x4y5

3．如图，已知直线l₁∥l₂，直线l₃和直线l₁，l₂交于点C和D，直线l₃上有一点P．
（1）如图1，若P点在C，D之间运动时，问∠PAC，∠APB，∠PBD之间的关系是否发生变化，并说明理由；
（2）若点P在C，D两点的外侧运动时（P点与点C，D不重合，如图2和3），试写出∠PAC，∠APB，∠PBD之间的关系，并说明理由．（图3只写结论，不写理由）

2．列方程组解应用题：
在“某地大地震”灾民安置工作中，某企业捐助了一批板材24 000m²，某灾民安置点用该企业捐助的这批板材全部搭建成A，B两种型号的板房，供2 300名灾民临时居住．已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示：

板房型号	所需板材	安置人数
A型板房	54m2	5
B型板房	78m2	8

问：（1）该灾民安置点需搭建A型板房和B型板房各多少间？
（2）因对灾民人数估计不足，实际安置中A型板房超员15%，B型板房超员20%，则该安置点灾民实际有多少人？

1．我们给出如下定义：两个图形G₁和G₂，在G₁上的任意一点P引出两条垂直的射线与G₂相交于点M、N，如果PM=PN，我们就称M、N为点P的垂等点，PM、PN为点P的垂等线段，点P为垂等射点．
（1）如图1，在平面直角坐标系xOy中，点P（1，0）为x轴上的垂等射点，过A（0，3）作x轴的平行线l，则直线l上的B（-2，3），C（-1，3），D（3，3），E（4，3）为点P的垂等点的是B（-2，3），E（4，3）；
（2）如果一次函数图象过M（0，3），点M为垂等射点P（1，0）的一个垂等点且另一个垂等点N也在此一次函数图象上，在图2中画出示意图并写出一次函数表达式；
（3）如图3，以点O为圆心，1为半径作⊙O，垂等射点P在⊙O上，垂等点在经过（3，0），（0，3）的直线上，如果关于点P的垂等线段始终存在，求垂等线段PM长的取值范围（画出图形直接写出答案即可）．

20．在体育中考项目中考生可在篮球、排球中选考一项．小明为了选择一项参加体育中考，将自己的10次测验成绩进行比较并制作了折线统计图，依据图中信息小明选择哪一项参加体育中考更合适，并说明理由，篮球，理由：篮球和排球的平均得分相同，但篮球发挥更稳定．

19．（1）定义：把四边形的某些边向两方延长，其他各边有不在延长所得直线的同一旁，这样的四边形叫做凹四边形．如图1，四边形ABCD为凹四边形．

（2）性质探究：请完成凹四边形一个性质的证明．
已知：如图2，四边形ABCD是凹四边形．
求证：∠BCD=∠B+∠A+∠D．
（3）性质应用：
如图3，在凹四边形ABCD中，∠BAD的角平分线与∠BCD的角平分线交于点E，若∠ADC=140°，∠AEC=102°，则∠B=64°．
（4）类比学习：
如图4，在凹四边形ABCD中，点E，F，G，H分别是边AD，AB，BC，CD的中点，顺次连接各边中点得到四边形EFGH．若AB=AD，CB=CD，则四边形EFGH是C．（填写序号即可）
A．梯形   B．菱形  C．矩形  D．正方形．

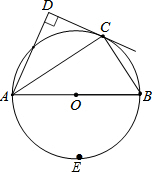18．如图，在四边形ABCD中，∠D=90°，AC平分∠DAB，且点C在以AB为直径的⊙O上．
（1）求证：CD是⊙O的切线；
（2）点E是⊙O上一点，连接BE，CE．若∠BCE=42°，cos∠DAC=$\frac{9}{10}$，AC=m，写出求线段CE长的思路．

17．阅读下列材料：2017年3月在北京市召开的第十二届全国人民代表大会第五次会议上，环境问题再次成为大家议论的重点内容之一．
北京自1984年开展大气监测，至2012年底，全市已建立监测站点35个.2013年，北京发布的首个PM_2.5年均浓度值为89.5微克/立方米．2014年，北京空气中的二氧化硫年均浓度值达到了国家新的空气质量标准；二氧化氮、PM₁₀、PM_2.5年均浓度值超标，其中PM_2.5年均浓度值为85.9微克/立方米．2016年，北京空气中的二氧化硫年均浓度值远优于国家标准；二氧化氮、PM₁₀、PM_2.5的年均浓度值分别为48微克/立方米、92微克/立方米、73微克/立方米．与2015年相比，二氧化硫、二氧化氮、PM₁₀年均浓度值分别下降28.6%、4.0%、9.8%；PM_2.5年均浓度值比2015年的年均浓度值80.6微克/立方米有较明显改善．（以上数据来源于北京市环保局）
根据以上材料解答下列问题：
（1）2015年北京市二氧化氮年均浓度值为50微克/立方米；
（2）请你用折线统计图将2013-2016年北京市PM_2.5的年均浓度值表示出来，并在图上标明相应的数据．