15．如果实数x，y满足$\sqrt{x+1}$+|y-2|=0，则xy的值是-2．

14．代数式$\sqrt{x+3}$有意义的条件是x≥-3．

13．在菱形ABCD中，AC，BD为对角线，下列说法一定正确的是（　　）

A．

AC=BD

B．

AC⊥BD

C．

∠ABD=∠BAC

D．

∠BAC+∠CAD=90°

12．已知?ABCD中，∠B=46°，则∠D的度数为（　　）

A．

44°

B．

46°

C．

72°

D．

144°

11．下面的四组数中的三个数值分别是三角形的三边长，能够成直角三角形的一组是（　　）

A．

1，$\sqrt{2}$，$\sqrt{3}$

B．

$\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$

C．

2，3，4

D．

6，7，8

10．下列计算正确的是（　　）

A．

$\sqrt{3}$+$\sqrt{6}$=3

B．

$\sqrt{2}$×$\sqrt{6}$=3$\sqrt{2}$

C．

$\sqrt{8}$÷$\sqrt{2}$=4

D．

（$\sqrt{12}$-$\sqrt{3}$）×$\sqrt{3}$=3

9．如图，在平面直角坐标系xOy中，直线y=-$\frac{3}{4}$x+3与x轴，y轴分别交于点A、B，点C的坐标为（0，-2），若点D在直线AB上运动，点E在直线AC上运动，当以O、A、D、E为顶点的四边形是平行四边形时，点D的坐标为（$\frac{12}{5}$，$\frac{6}{5}$）或（$\frac{28}{5}$，-$\frac{6}{5}$）．

8．城市规划期间，欲拆除一电线杆AB，如图，已知大坝背水坡ED的坡角∠EDG=60°，背水坡ED的垂直高度EH为6米，在坝顶E处有一高为1米的测角仪EF，测得杆顶A的仰角为20°，杆底B的俯角为20°，C、D之间是2米宽的人行道，在拆除电线杆AB时，为确保行人安全，是否需要将此人行道封闭？请说明理由（在地面上，以点B为圆心，以AB为半径的圆形区域为危险区域）．（tan20°≈0.4，tan70°≈2.7，$\sqrt{3}$≈1.7）

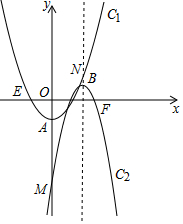7．如图，抛物线C₁：y₁=tx²-1（t＞0）和抛物线C₂：y₂=-4（x-h）²+1（h≥1）．
（1）两抛物线的顶点A、B的坐标分别为（0，1）和（h，1）；
（2）设抛物线C₂的对称轴与抛物线C₁交于点N，则t为何值时，A、B、M、N为顶点的四边形是平行四边形．
（3）设抛物线C₁与x轴的左交点为点E，抛物线C₂与x轴的右边交点为点F，试问，在第（2）问的前提下，四边形AEBF能否为矩形？若能，求出h值；若不能，说明理由．

6．菲尔兹奖是国际上有崇高声誉的一个数学奖项，下面的数据是从1936年至2014年菲尔兹奖得主获奖时的年龄（岁）：
                       29  39  35  33  39  27  33  35  31  31  37  32  38  36
                       31  39  32  38  37  34  29  34  38  32  35  36  33  32
                       29  35  36  37  39  38  40  38  37  39  38  34  33  40
                       36  36  37  40  31  38  38  40  40  37  35  40  39  37
请根据上述数据，解答下列问题：
小彬按“组距为5”列出了如图的频数分布表

分组	频数
A：25～30	4
B：30～35	15
C：35～40	31
D：40～45	6
合计	56

（1）每组数据含最小值不含最大值，请将表中空缺的部分补充完整，并补全频数分布直方图；
（2）根据（1）中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征；
（3）在（1）的基础上，小彬又画了如图所示的扇形统计图，图中获奖年龄在30～35岁的人数约占获奖总人数的26.8%（百分号前保留1位小数）；C组所在扇形对应的圆心角度数约为199°（保留整数）