科目： 来源： 题型：选择题

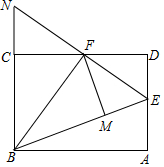3．如图，在矩形ABCD中，点E是AD的中点，∠EBC的平分线奇交CD于点F，将△DEF沿EF折叠，点D恰好落在BE上M点处，延长BC、EF交于点N，有下列四个结论：
①DF=CF；②BF⊥EN；③S_△BEF=3S_△DEF；④CN=DE．
其中，将正确的结论有几个：（　　）

A．

2

B．

3

C．

4

D．

5

科目： 来源： 题型：选择题

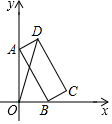2．如图，矩形ABCD中，AB=8，BC=3，顶点A，B分别在y轴和x轴上，当点A在y轴上移动时，点B也随之在x轴上移动，在移动过程中，OD的最大值为（　　）

A．

8

B．

$\sqrt{73}$

C．

$\sqrt{85}$

D．

9

科目： 来源： 题型：选择题

1．如图，把矩形ABCD沿EF折叠，点B恰好落在AD边的B′处，若AE=2，DE=6，∠EFB=60°，则矩形ABCD的面积是（　　）

A．

16$\sqrt{3}$

B．

24

C．

12$\sqrt{3}$

D．

12

科目： 来源： 题型：解答题

科目： 来源： 题型：选择题

19．如图，一个质点在第一象限及x轴，y轴上运动，在第一秒钟，它从原点（0，0）运动到（0，1），然后接着按图中箭头所示方向运动，即（0，0）→（0，1）→（1，1）→（1，0）→…，且每秒移动一个单位，那么第24秒时质点所在位置的坐标是（　　）

A．

（0，5）

B．

（5，0）

C．

（0，4）

D．

（4，0）

科目： 来源： 题型：解答题

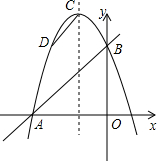18．如图，一次函数y=x+3的图象与坐标轴分别交于A，B两点，二次函数y=ax²+bx-3a的图象经过点A，B．
（1）求二次函数y=ax²+bx-3a的表达式．
（2）设此抛物线顶点为C，点B关于抛物线对称轴的对称点为D，求证：CD∥AB．
（3）试问直线AB上是否存在点P，使得△BDP与△BCD相似？若存在，求出点P的坐标；若不存在，请说明理由．

科目： 来源： 题型：解答题

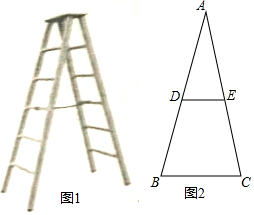17．如图1所示的是由梯子AB和梯子AC搭成的“人字梯”，它的5个踩档把梯子等分成6份，梯子的第三踩档处有一条绑绳DE，将其抽象成图2，其中AB=AC=2米．
（1）若DE的长为60厘米，求两梯角之间的距离BC的长．
（2）若∠ABC=70°，小明想在人字梯的D，E处系上一根绳子确保用梯安全，在D，E处打结各需要0.3米的绳子，请你帮小明计算一下，他需要的绑绳的长度为多少米？此时梯子的顶端A离地面BC的高度为多少米？（结果精确到0.01厘米；参考数据：sin70°=0.9397，cos70°=0.3420，tan70°=2.7475）

科目： 来源： 题型：填空题

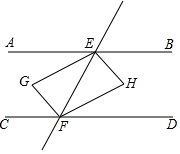16．如图，直线AB∥CD，EG平分∠AEF，HE⊥GE于E，且平移EH恰好到GF，则下列结论：①EH平分∠BEF；②EG=HF；③FH平分∠EFD；④∠GFH=90°，其中一定正确的结论有4个．

科目： 来源： 题型：解答题

15．已知△ABC的三边长分别为AB=2$\sqrt{5}$，AC=2，BC=4$\sqrt{\frac{1}{2}}$．
（1）在如图所示的5×5方格内画出△ABC，并使其顶点都在格点上；
（2）求S_△ABC及最长边上的高．

科目： 来源： 题型：解答题

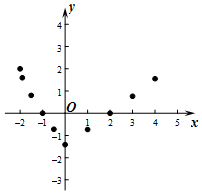14．有这样一个问题：探究函数y=-$\sqrt{x+2}$+|x|的图象与性质．?
小军根据学习函数的经验，对函数y=-$\sqrt{x+2}$+|x|的图象与性质进行了探究．
下面是小军的探究过程，请补充完整：
（1）函数y=-$\sqrt{x+2}$+|x|的自变量x的取值范围是x≥-2；
（2）表是y与x的几组对应值?

x	-2	-1.9	-1.5	-1	-0.5	0	1	2	3	4	…
y	2	1.60	0.80	0	-0.72	-1.41	-0.37	0	0.76	1.55	…

在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（3）观察图象，函数的最小值是-$\sqrt{2}$；
（4）进一步探究，结合函数的图象，写出该函数的一条性质（函数最小值除外）：当-2≤x＜0时，y随x的增大而减小．