
科目: 来源: 题型:选择题
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | 1 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
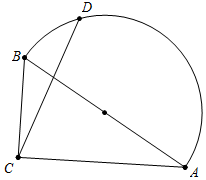 如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )
如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )| A. | π或$\frac{π}{2}$ | B. | $\frac{π}{2}$或$\frac{π}{3}$ | C. | $\frac{π}{3}$或π | D. | $\frac{π}{4}$或$\frac{π}{3}$ |
查看答案和解析>>
科目: 来源: 题型:填空题
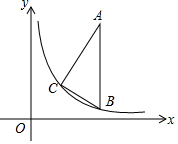 如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.
如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.查看答案和解析>>
科目: 来源: 题型:解答题
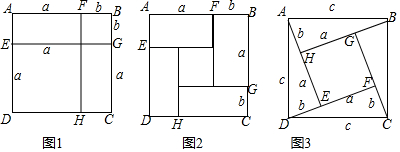
查看答案和解析>>
科目: 来源: 题型:解答题
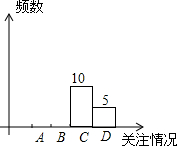 2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.
2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.| 关注情况 | 频数 | 频率 |
| A.高度关注 | k | 0.2 |
| B.一般关注 | m | 0.5 |
| C.极少关注 | 10 | n |
| D.不关注 | 5 | 0.1 |
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com