20．如果实数x满足（x+$\frac{1}{x}$）²-（x+$\frac{1}{x}$）-2=0，那么x+$\frac{1}{x}$的值是2或-1．

19．在平面直角坐标系xOy（如图）中，已知点A的坐标为（3，1），点B的坐标为（6，5），点C的坐标为（0，5）；某二次函数的图象经过点A、点B与点C．
（1）求这个二次函数的解析式；
（2）假如点Q在该函数图象的对称轴上，且△ACQ是等腰三角形，直接写出点Q的坐标；
（3）如果第一象限内的点P在（1）中求出的二次函数的图象上，且tan∠PCA=$\frac{1}{2}$，求∠PCB的正弦值．

18．近年来，我国很多地区持续出现雾霾天气，某市记者为了了解“雾霾天气的主要成因”，随机调查了该市部分市民，并对调查结果进行整理，绘制了如下尚不完整的统计图表．

组别	观点	频数
A	大气气压低，空气不流动	m
B	地面灰尘大，空气湿度低	20
C	汽车尾气排放	n
D	工厂造成的污染	80
E	其他	30

请根据图表中提供的信息解答下列问题：
（1）m=10，n=60，扇形统计图中E组所占的百分比为15%；
（2）若该市人口约为600万人，请你估计其中持D组“观点”的市民人数；
（3）对于“雾霾”这个环境问题，请结合上面的统计情况，用简短的语言发出倡议．

17．阅读下面的文字，解答问题
大家知道$\sqrt{2}$是无理数，而无理数是无限不循环小数，因此$\sqrt{2}$的小数部分我们不可能全部地写出来，但是由于
1＜$\sqrt{2}$＜2，所以$\sqrt{2}$的整数部分为1，将$\sqrt{2}$减去其整数部分1，所得的差就是其小数部分$\sqrt{2}$-1，根据以上的内容，解答下面的问题：
（1）$\sqrt{5}$的整数部分是2，小数部分是$\sqrt{5}$-2；
（2）1+$\sqrt{2}$的整数部分是2，小数部分是$\sqrt{2}$-1；
（3）1+$\sqrt{2}$+$\sqrt{3}$整数部分是4，小数部分是$\sqrt{2}$+$\sqrt{3}$-3；
（4）若设2+$\sqrt{3}$整数部分是x，小数部分是y，求x-$\sqrt{3}$y的值．

16．如图，已知A（m，3）是一次函数y=kx+b与反函数y=$\frac{6}{x}$（x＞0）的交点．
（1）求m的值；
（2）若一次函数分别与x、y轴交于E、F两点，A为EF的中点，试求该一次函数的解析式；
（3）在y=$\frac{6}{x}$的图象上另取一点B，作BK⊥x轴于K，在（2）的条件下，在y轴上取一点C，使得FO=4CO．问：在y轴上是否存在点P，使得△PAC和△PBK的面积相等？若存在，求出点P的坐标，若不存在，请说明理由．

15．某商品的进价为每件40元，当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件，在确保盈利的前提下，解答下列问题：
（1）求降价前每星期的销售利润；
（2）若设每件降价x元，每星期售出商品的利润为y元，请写出y与x的函数关系式，并直接写出自变量x的取值范围；
（3）当降价多少元时，每星期的利润最大？最大利润是多少？

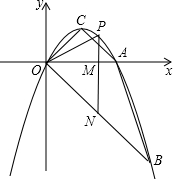14．如图，抛物线y=ax²+bx经过A（2，0），B（3，-3）两点，抛物线的顶点为C，动点P在直线OB上方的抛物线上，过点P作直线PM∥y轴，交x轴于M，交OB于N，设点P的横坐标为m．
（1）求抛物线的解析式及点C的坐标；
（2）当△PON为等腰三角形时，点N的坐标为（1，-1），（2，-2），（3-$\sqrt{2}$，$\sqrt{2}$-3）；当△PMO∽△COB时，点P的坐标为（$\frac{5}{3}$，$\frac{5}{9}$），（$\frac{7}{3}$，-$\frac{7}{9}$）；（直接写出结果）
（3）直线PN能否将四边形ABOC分为面积比为1：2的两部分？若能，请求出m的值；若不能，请说明理由．

13．已知△ABC中，AB=AC，D为直线BC上一点．
（1）如图1，BH⊥AD于H，若AD=BD，求$\frac{AH}{BC}$的值；
（2）如图2，∠BAC=90°，E为AB的中点，∠BCE=∠DAB，BD=2，求CE的长；
（3）如图3．∠BAC=60°，F为AC上一点，AF=2CF，∠FDC=∠ABF，延长DF至G，使GF=BF，求证AG∥BC．

12．已知函数y=x+b的图象与坐标轴围成的三角形面积为1，则b=（　　）

A．

±$\sqrt{2}$

B．

±2

C．

2

D．

$\sqrt{2}$

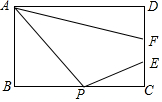11．如图，在矩形ABCD中，AB=6，AD=8，点P是BC中点，点E、F是边CD上的任意两点，且EF=2，当四边形APEF的周长最小时，则DF的长为（　　）

A．

2

B．

4

C．

$\frac{8}{3}$

D．

$\frac{10}{3}$