
科目: 来源: 题型:解答题
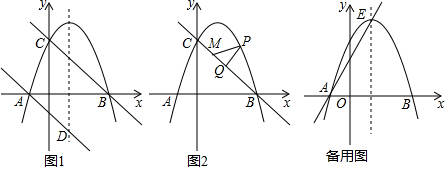
查看答案和解析>>
科目: 来源: 题型:填空题
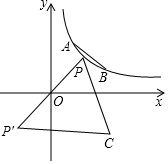 如图点A(1,2)、B(2,1)在反比例函数y=$\frac{2}{x}$图象上,点P是反比例函数y=$\frac{2}{x}$在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.
如图点A(1,2)、B(2,1)在反比例函数y=$\frac{2}{x}$图象上,点P是反比例函数y=$\frac{2}{x}$在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.查看答案和解析>>
科目: 来源: 题型:选择题
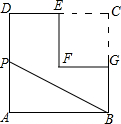 如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )
如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )| A. | 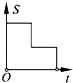 | B. | 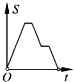 | C. | 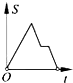 | D. | 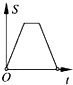 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
| 方式一 | 方式二 | |
| 月租费/(元/月) | 30 | 0 |
| 本地通话费/(元/min) | 0.30 | 0.40 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
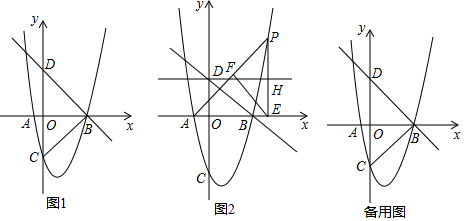
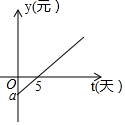 某地蔬菜市场采用如下经营模式:个体蔬菜经营商向市场管理部门租赁摊位,每月缴纳一定的“摊位费”(含市场管理等费用),蔬菜市场管理公司靠收每户的“摊位费”盈利,个体经营商每经营一天,平均可得“营业额”800元,但平均每天要支付蔬菜的“进货费”400元,如图是某个体蔬菜经营商经营一个月(均按30天计算)的收益(除去“摊位费”和“进货费”)y元随经营时间t天变化的函数图象.
某地蔬菜市场采用如下经营模式:个体蔬菜经营商向市场管理部门租赁摊位,每月缴纳一定的“摊位费”(含市场管理等费用),蔬菜市场管理公司靠收每户的“摊位费”盈利,个体经营商每经营一天,平均可得“营业额”800元,但平均每天要支付蔬菜的“进货费”400元,如图是某个体蔬菜经营商经营一个月(均按30天计算)的收益(除去“摊位费”和“进货费”)y元随经营时间t天变化的函数图象.查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
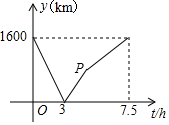 【情景】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),相距y(km)与时间t(h)满足的数量关系如图所示.
【情景】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),相距y(km)与时间t(h)满足的数量关系如图所示.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com