练习册

  • 练习册
  • 试题
    相关习题
     0  295728  295736  295742  295746  295752  295754  295758  295764  295766  295772  295778  295782  295784  295788  295794  295796  295802  295806  295808  295812  295814  295818  295820  295822  295823  295824  295826  295827  295828  295830  295832  295836  295838  295842  295844  295848  295854  295856  295862  295866  295868  295872  295878  295884  295886  295892  295896  295898  295904  295908  295914  295922  366461 

    科目： 来源： 题型：解答题

    6．某班30名同学在“献爱心”活动中都捐赠了图书，各人捐赠的本数如下5，2，4，5，3，2，4，3，5，4，3，4，2，3，3，4，4，5，3，4，3，5，3，5，3，4，3，4，3，3．
    （1）填写全班同学捐书册数统计表中未完成的部分．
    （2）画出扇形统计图，描述分别捐赠2册、3册、4册和5册图书的人数占全班同学的百分比．
     捐书册数划记  人数 百分比
     2  3 10%
     312 40% 
     4  9 30%
     5620% 

    查看答案和解析>>

    科目： 来源： 题型：解答题

    5．自来水公司规定：月用水量低于800t的，按每吨4元收取水费；用水量超过800t但低于1200t的部分增收10%的增容费．
    （1）当月用水量低于800t时，写出应缴水费y（元）与用水量x（t）之间的函数关系式．
    （2）当月用水量超过800t而低于1200t时，写出应缴水费y（元）与用水量x（t）之间的函数关系式．
    （3）若第三中学上月交水费3640元，则该中学上月用水多少？

    查看答案和解析>>

    科目： 来源： 题型：解答题

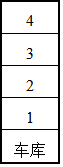    4．小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯，已知两个陌生人到1至4层的任意一层出电梯．
    （1）用列表法或画树状图法帮小明求出甲、乙二人在同一层楼出电梯的概率；
    （2）小亮和小芳打赌说：“若甲、乙二人在同一层或相邻楼层出电梯，则小亮胜，否则小芳胜”，该游戏规则是否公平？若公平，说明理由，若不公平，请修改游戏规则，是游戏公平．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    3．化简：
    （1）$\root{4}{（a-b）^{4}}$
    （2）$\frac{\root{5}{{a}^{2}}}{\root{3}{a}•\root{15}{a}}$
    （3）$（8{a}^{6}{b}^{-9}）^{-\frac{2}{3}}$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

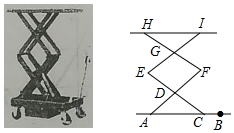    2．如图是某科技馆展览的一个升降平台模型，在其示意图中，AB=AF=CE=EI=FH=50cm，其中点D是AF和CE的中点，点G是EI和FH的中点．当点C在线段AB上滑动时，∠DAC的大小随之发生变化，平台的高度也随之发生变化，从而控制平台面HI的升降．
    （1）HI与AC平行吗？请说明理由．
    （2）移动点C的位置，当∠DAC的大小由30°变化到60°时，平台上升了多少？（结果精确到0.1cm）（可使用科学计算器．参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）

    查看答案和解析>>

    科目： 来源： 题型：解答题

    1．已知y与x-2成正比例，且x=3时，y=-2．
    （1）求出y与x的函数关系式．
    （2）在平面直角坐标系中画出（1）中函数的大致图象．
    （3）求此函数图象与两坐标轴围成的三角形面积．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    20．由于连续下雨，水位不断上涨．下表记录了5个时间段的桥面到水面的距离：
    x（h）01234…
    y（m）109.598.58…
    （1）由记录表写出y随x变化的函数解析式；
    （2）画出这个函数图象；
    （3）据估计，这种上涨的俯况还会持续，一船水上部分高4m，下雨时距离此桥还有16小时的路．
    ①此船按原速前进能否通过此桥？为什么？
    ②若此船原来速度为每小时24千米，为了顺利通过此桥，请你给船长提一个合理的建议．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    19．如图，在平面直角坐标系xOy中，边长为4的正方形OABC的顶点A在x轴上，顶点C在y轴上，点D是OA的中点，连接CD，过D作DE⊥CD，且DE=CD，以点D为顶点的抛物线刚好经过E点，P为射线CB上一点，过点P作PF⊥CD于点F．
    （1）求E点坐标及抛物线的表达式；
    （2）若点P从点C出发，沿射线CB以每秒1个单位长度的速度运动，运动时间为t秒．则当t为何值时，以点P，F，D为顶点的三角形与△COD相似？
    （3）点Q为抛物线上一点，当点Q在直线PF上，且满足以点D，E，P，Q为顶点的四边形是平行四边形时，求点Q的坐标．

    查看答案和解析>>

    科目： 来源： 题型：填空题

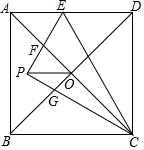    18．如图，在边长为4的正方形ABCD中，对角线AC，BD相交于点O，点E是AD边上一点，连接CE，把△CDE沿CE翻折，得到△CPE，EP交AC于点F，CP交BD于点G，连接PO，若PO∥BC，则四边形OFPG的面积是8-4$\sqrt{3}$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    17．先化简，再求代数式（$\frac{2}{a+1}$-$\frac{2a-3}{{a}^{2}-1}$）÷$\frac{1}{a+1}$的值，其中a=$\sqrt{2}$+1．

    查看答案和解析>>

    同步练习册答案