
科目: 来源: 题型:解答题
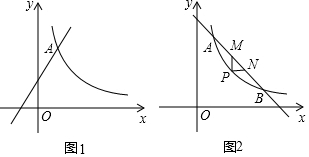
查看答案和解析>>
科目: 来源: 题型:解答题
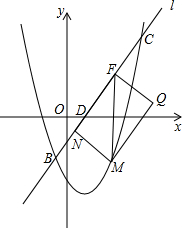 已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).
已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).查看答案和解析>>
科目: 来源: 题型:解答题
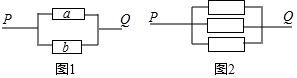 在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能;通电或断开,并且这种状态的可能性相等.
在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能;通电或断开,并且这种状态的可能性相等.查看答案和解析>>
科目: 来源: 题型:选择题
| A. |  | B. |  | C. | 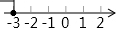 | D. | 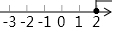 |
查看答案和解析>>
科目: 来源: 题型:选择题
| 班级 | 参加人数 | 中位数 | 方差 | 平均数 |
| (1)班 | 50 | 120 | 103 | 122 |
| (2)班 | 49 | 121 | 201 | 122 |
| A. | 两班平均成绩一样 | B. | (1)班的优秀人数多于(2)班 | ||
| C. | (2)班的两极分化比(1)班严重 | D. | (1)班的总体成绩稳定一些 |
查看答案和解析>>
科目: 来源: 题型:选择题
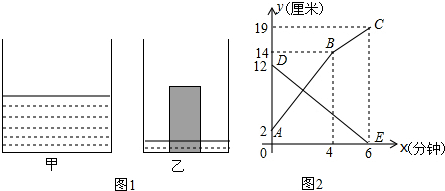
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目: 来源: 题型:解答题
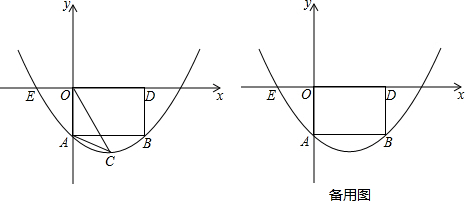
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com