7．小麦与小辉在玩游戏，他们定义了一种新的规则，用象棋的“相”“仕”“帅”“兵”来比较大小，共有8个棋子：2个“相”，2个“仕”，1个“帅”，3个“兵”．

游戏规则如下：
①游戏时，将棋子反面朝上，两人随机各摸一个棋子进行比赛称一轮比赛，先摸者摸出的棋子不放回；
②“相”胜“兵”；“仕”胜“相”、“兵”；“帅”胜“相”、“仕”；“兵”胜“帅”；
③相同棋子不分胜负．
（1）若小麦先摸到了“仕”，小辉在剩余的7只棋中随机摸一只，问这一轮中小麦胜小辉的概率是多少？
（2）若进行一轮游戏，小麦先摸棋子，求小麦获胜的概率．

6．如图，我区某中学开展“健康运动”的活动，决定开设“A：乒乓球，B：拔河，C：跳绳，D：篮球”四种运动项目，为了解学生最喜欢哪一种运动项目（每位同学均只选择一项），随机抽取了九年级部分学生，根据调查结果绘制成如图的统计图：
（1）本次共调查了200学生，其中最喜欢跳绳运动项目的学生数为40人；在扇形图中，最喜欢拔河的对应扇形的圆心角大小是54度；
（2）根据以上统计分析，在这四种“健康运动”项目中，学生最喜欢的运动项目是什么？并估计该校1200名学生中喜欢此项目的学生人数．

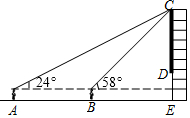5．如图是某市中心一家大型购物商城墙面上的电子屏幕，好学的小希想利用所学的知识测量电子屏幕上下端之间的高度，于是她站在屏幕正前方的点A处，测得电子屏幕上端C处的仰角为24°，接着他正对电子屏幕方向前进7m到达点B处，又测得电子屏幕上端C处的仰角为58°，已知图中所有点均在同一平面内，小希的眼睛始终距离地面1.60m，CE⊥AE，DE=3m，请你根据以上测量数据，求该电子屏幕上下端之间的高度CD．（参考数据：sin24°≈0.41，cos24°≈0.91，tan24°≈0.45，sin58°≈0.85，cos58°≈0.53，tan58°≈1.60，结果精确到0.1m）

4．计算：$\sqrt{4}$-（-5）+|1-2sin²60°|+$\root{3}{-\frac{1}{8}}$．

3．为增强学生的爱国意识，某中学举办“爱我中华”朗诵比赛，全校学生都参加，并对表现优异的学生进行表彰，设置一、二、三等奖和进步奖共四个奖项，赛后，校统计小组随机抽取了九年级两个班级，并将这两个班的获奖情况绘制成以下两幅不完整的统计图．
请根据图中的信息，解答下列问题：
（1）求本次调查抽取的学生人数，并补全条形统计图；
（2）在扇形统计图中，表示“三等奖”的扇形所对应的圆心角度数是72°．
（3）若该校共有2600名学生，试估计得奖的学生人数．

2．计算：|-3|-（π-3.14）⁰+$\sqrt{8}$-2cos45°．

1．在平面直角坐标系xOy，直线y=x-1与y轴交于点A，与双曲线y=$\frac{k}{x}$交于点B（m，2）
（1）求点B的坐标及k的值；
（2）将直线AB平移，使它与x轴交于点C，与y轴交于点D，若△ABC的面积为6，求直线CD的表达式．

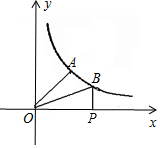20．如图，已知A、B是反比例函数y=$\frac{k}{x}$图象上两点，BP⊥x轴，垂足为P．
已知∠AOP=45°，OA=4，tan∠BOP=$\frac{1}{2}$．
（1）求点A的坐标；
（2）连接AB，求四边形AOPB的面积．

19．【问题探究】
已知：如图①所示，∠MPN的顶点为P，⊙O的圆心O从顶点P出发，沿着PN方向平移．

（1）如图②所示，当⊙O分别与射线PM，PN相交于A、B、C、D四个点，连接AC、BD，可以证得△PAC∽△△PDB，从而可以得到：PA•P B=P C•P D．
（2）如图③所示，当⊙O与射线PM相切于点A，与射线PN相交于C、D两个点．求证：PA²=PC•PD．
【简单应用】
（3）如图④所示，（2）中条件不变，经过点P的另一条射线与⊙O相交于E、F两点．利用上述（1），（2）两问的结论，直接写出线段PA与PE、PF之间的数量关系PA²=PE•PF；当PA=4$\sqrt{3}$，EF=2，则PE=6．
【拓展延伸】
（4）如图⑤所示，在以O为圆心的两个同心圆中，A、B是大⊙O上的任意两点，经过A、B 两点作线段，分别交小⊙O于C、E、D、F四个点．求证：AC•AE=BD•BF．（友情提醒：可直接运用本题上面所得到的相关结论）

18．已知二次函数y=-x²+2mx-2m²-3（m为常数）．
（1）求证：不论m为何值，该二次函数图象与x轴没有公共点；
（2）如果把该函数图象沿y轴向上平移4个单位后，得到的函数图象与x轴只有一个公共点，试求m的值．