
科目: 来源: 题型:解答题
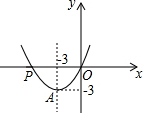 已知抛物线y=ax2+bx经过点A(-3,-3)和点P(m,0),且m≠0.
已知抛物线y=ax2+bx经过点A(-3,-3)和点P(m,0),且m≠0.查看答案和解析>>
科目: 来源: 题型:选择题
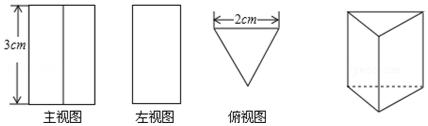
| A. | 18cm2 | B. | 20cm2 | C. | (18+2$\sqrt{3}$)cm2 | D. | (18+4$\sqrt{3}$)cm2 |
查看答案和解析>>
科目: 来源: 题型:解答题
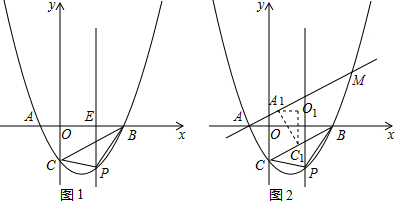
查看答案和解析>>
科目: 来源: 题型:解答题
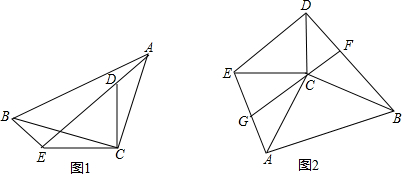
查看答案和解析>>
科目: 来源: 题型:解答题
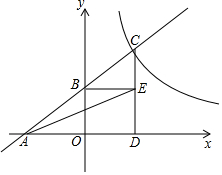 如图,直线AB与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k>0)交于点C,过点C作CD⊥x轴于点D,过点B作BE⊥CD于点E,tan∠BCE=$\frac{3}{2}$,点E的坐标为(2,$\frac{3}{2}$),连接AE.
如图,直线AB与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$(k>0)交于点C,过点C作CD⊥x轴于点D,过点B作BE⊥CD于点E,tan∠BCE=$\frac{3}{2}$,点E的坐标为(2,$\frac{3}{2}$),连接AE.查看答案和解析>>
科目: 来源: 题型:选择题
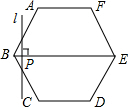 如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )
如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )| A. | 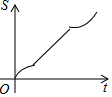 | B. |  | C. | 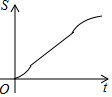 | D. | 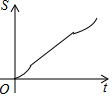 |
查看答案和解析>>
科目: 来源: 题型:解答题
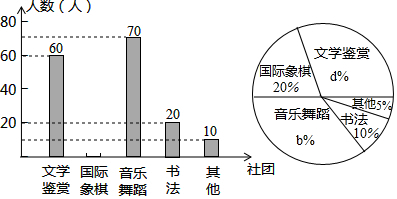
查看答案和解析>>
科目: 来源: 题型:解答题
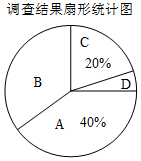 某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:
某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:| 组别 | 上学常用的一种交通方式 | 频数(人数) |
| A | 步行 | 64 |
| B | 骑自行车 | m |
| C | 乘公交车 | n |
| D | 其它 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com