
科目: 来源: 题型:解答题
| 甲种糖果 | 乙种糖果 | 丙种糖果 | |
| 单价(元/千克) | 20 | 25 | 30 |
| 千克数 | 40 | 40 | 20 |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 2a-3a=a | B. | (a3)2=a6 | C. | $\sqrt{-2a}$=$\sqrt{-2}$×$\sqrt{a}$ | D. | a6÷a3=a2 |
查看答案和解析>>
科目: 来源: 题型:选择题
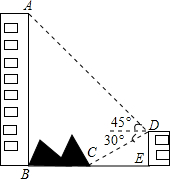 如图,大楼AB的右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离是( )
如图,大楼AB的右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离是( )| A. | 50 | B. | 70-10$\sqrt{3}$ | C. | 70+10$\sqrt{3}$ | D. | 70-$\frac{10\sqrt{3}}{3}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,利用热气球探测器测量大楼AB的高度,从热气球P处测得大楼B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离底面的高度为120m.试求大楼AB的高度(结果保留整数).
如图,利用热气球探测器测量大楼AB的高度,从热气球P处测得大楼B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离底面的高度为120m.试求大楼AB的高度(结果保留整数).查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 数据3、5、4、1、-2的中位数是3 | |
| B. | 数据1、1、0、2、4的平均数是2 | |
| C. | 在选举中,人们通常最关心是数据的众数 | |
| D. | 甲乙两人近5次数学考试平均分都是95分,方差分别是2.5和8.5,要选一人参加数学竞赛,选甲比较合适 |
查看答案和解析>>
科目: 来源: 题型:解答题
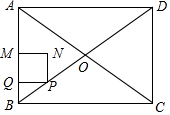 如图,矩形ABCD的对角线相交于点O,AB=6cm,BC=8cm,动点P以1cm/s的速度从点B出发,沿B→O→C向终点C运动,当点P在OB上运动时,过点P作PQ⊥AB于点Q,以PQ为边向上方作正方形PQMN,当点P在OC上运动时,过点P作PQ∥AB交OD于点Q,以PQ为边向左侧作正方形PQMN,设正方形PQMN与△ABO重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,矩形ABCD的对角线相交于点O,AB=6cm,BC=8cm,动点P以1cm/s的速度从点B出发,沿B→O→C向终点C运动,当点P在OB上运动时,过点P作PQ⊥AB于点Q,以PQ为边向上方作正方形PQMN,当点P在OC上运动时,过点P作PQ∥AB交OD于点Q,以PQ为边向左侧作正方形PQMN,设正方形PQMN与△ABO重叠部分图形的面积为S(cm2),点P运动的时间为t(s).查看答案和解析>>
科目: 来源: 题型:解答题
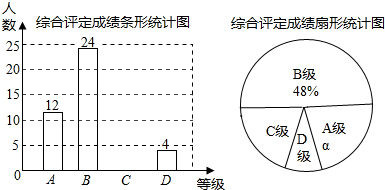
查看答案和解析>>
科目: 来源: 题型:解答题
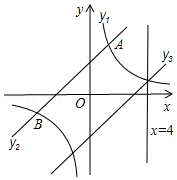 如图所示,在同一直角坐标系xOy中,有双曲线y1=$\frac{{k}_{1}}{x}$,直线y2=k2x+b1,y3=k3x+b2,且点A(2,5),点B(-6,n)在双曲线的图象上
如图所示,在同一直角坐标系xOy中,有双曲线y1=$\frac{{k}_{1}}{x}$,直线y2=k2x+b1,y3=k3x+b2,且点A(2,5),点B(-6,n)在双曲线的图象上查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com