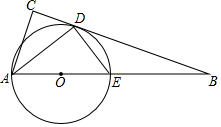16．如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以OA为半径的⊙O经过点D，与AB交于点E．
（1）求证：BD²=BE•BA；
（2）若cosB=$\frac{{2\sqrt{2}}}{3}$，AE=4，求CD．

15．分解因式2x²-$\frac{1}{2}$=$\frac{1}{2}$（2x+1）（2x-1）．

14．我区某校为了更好地开展学生课外体育运动，学校决定用1600元购进排球8个，篮球14个，已知每个篮球的售价比排球的售价多20元．
（1）每个排球、篮球的售价分别为多少元；
（2）若学校打算再次购进两种球共30个，且购买的30个球中排球的总金额不低于篮球的总金额，若排球、篮球的进价分别为50元、65元，则在第二次购买活动中，商家最多能获利多少？

13．新房装修后，甲居民购买家居用品的清单如下表，因污水导致部分信息无法识别，根据下表解决问题：

家居用品名称	单价（元）	数量（个）	金额（元）
挂钟	30	2	60
垃圾桶	15
塑料鞋架	40
艺术字画	a	2	90
电热水壶	35	1	b
合计		8	280

（1）直接写出a=45，b=35；
（2）甲居民购买了垃圾桶，塑料鞋架各几个？
（3）若甲居民再次购买艺术字画和垃圾桶两种家居用品，共花费150元，则有哪几种不同的购买方案？

12．无锡某校准备组织学生及学生家长到上海进行社会实践，为了便于管理，所有人员必须乘坐在同一列火车上：根据报名人数，若都买一等座单程火车票需17010元，若都买二等座单程火车票且花钱最少，则需11220元；已知学生家长与教师的人数之比为2：1，无锡到上海的火车票价格（部分）如表所示：

运行区间		公布票价		学生票价
上车站	下车站	一等座	二等座	三等座
无锡	上海	81（元）	68（元）	51（元）

（1）参加社会实践的老师、家长与学生各有多少人？
（2）由于各种原因，二等座火车票单程只能买m张（m小于参加社会实践的人数），其余的须买一等座火车票，在保证每位参与人员都有座位坐的前提下，请你设计最经济的购票方案，并写出购买火车票的总费用（单程）w与m之间的函数关系式．
（3）按第（2）小题中的购票方案，请你做一个预算，购买这次单程火车票最少要花多少钱？最多要花多少钱？

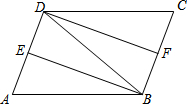11．如图，在?ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．
（1）求证：△ABE≌△CDF；
（2）若AB=DB，猜想：四边形DFBE是什么特殊的四边形？并说明理由．

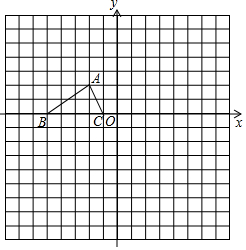9．如图，已知△ABC的三个顶点的坐标分别为A（-2，2）、B（-5，0）、C（-1，0），P（a，b）是△ABC的边AC上一点：
（1）将△ABC绕原点O逆时针旋转90°得到△A₁B₁C₁，请在网格中画出△A₁B₁C₁，旋转过程中点A所走的路径长为 $\sqrt{2}$π．
（2）将△ABC沿一定的方向平移后，点P的对应点为P₂（a+6，b+2），请在网格画出上述平移后的△A₂B₂C₂，并写出点A₂的坐标：A₂（4，4）．
（3）若以点O为位似中心，作△A₃B₃C₃与△ABC成2：1的位似，则与点P对应的点P₃位似坐标为（2a，2b）或（-2a，-2b）（直接写出结果）．

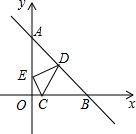8．如图，已知点C（1，0），直线y=-x+7与两坐标轴分别交于A、B两点，D、E分别是AB，OA上的动点，当△CDE周长最小时，点D坐标为（$\frac{25}{7}$，$\frac{24}{7}$）．

7．在平面直角坐标系中，我们不妨把横坐标与纵坐标相等的点称为梦之点，例如，点（1，1），（-2，-2），（ $\sqrt{2}$，$\sqrt{2}$  ），…，都是梦之点，显然梦之点有无数个．
（1）若点P（2，b）是反比例函数y=$\frac{n}{x}$（n为常数，n≠0）的图象上的梦之点，求这个反比例函数解析式；
（2）⊙O的半径是$\sqrt{2}$，
①求出⊙O上的所有梦之点的坐标；
②已知点 M（m，3），点Q是（1）中反比例函数y=$\frac{n}{x}$图象上异于点P的梦之点，过点Q 的直线l与y轴交于点 A，tan∠OAQ=1．若在⊙O上存在一点N，使得直线MN∥l或MN⊥l，求出m的取值范围．