5．【发现】：如图1，在正三角形ABC中，在AB，AC边上分别取点M，N，BM=AN，连接BN，CM，相交于点O，求∠α
易得：△ABN≌△BCN，则∠1=∠2
∵∠α是△BOC的外角，∴∠α=∠2+∠3
∴∠α=∠1+∠3=∠ABC=60°

【推广】：在正n边形中，对相邻的两边实施同样的操作…
（1）如图2，在正四边形ABCD中，在AB，AD边上分别取点M，N，连接BN，CM，可确定∠α=90°；
（2）如图3，在正五边形ABCDE中，在AB，AD边上分别取点M，N，连接BN，CM，可确定∠α=108°；
（3）判断：∠α可以等于160°吗？如果可以，求出对应的边数n，若不可以，说明理由．

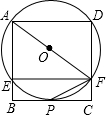4．如图，正方形ABCD顶点A，D在⊙O上，边BC经过⊙O上一定P，且PF平分∠AFC，边 AB，CD分别与⊙O相交于点E、F，连接EF．
（1）求证：BC是⊙O的切线；
（2）若FC=2，求PC的长．

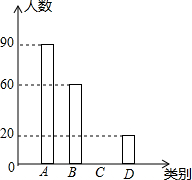3．雾霾天气已经成为人们普遍关注的话题，雾霾不仅仅影响人们的出行，还影响着人们的健康．在2017年2月周末休息期间，某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题，随机调查了太原市部分市民的观点，并对调查结果进行了整理，绘制了如下不完整的统计表及统计图，观察并回答下列问题：

类别	雾霾天气的主要成因	百分比
A	工业污染	45%
B	汽车尾气排放	m
C	城中村燃煤问题	15%
D	其他（绿化不足等）	n

（1）请你求出本次被调查市民的人数及m，n的值，并补全条形统计图；
（2）若该市有800万人口，请你估计持有B，C两类看法的市民共有多少人？
（3）小明同学在四个质地、大小、形状都完全相同的小球上标记A，B，C，D代表四个雾霾天气的主要成因中，放在一个不透明的盒子中，他先随机抽取一个小球，放回去，再随机抽取一个小球，请用画树状图或列表的方法，求出小颖同学刚好抽到B和D的概率．（用A，B，C，D表示各项目）

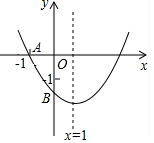2．如图，已知二次函数y=ax²+bx+c（a≠0）的图象与x轴交于点A（-1，0），与y轴的交点B在（0，-2）和（0，-1）之间（不包括这两点），对称轴为直线x=1，下列结论：①abc＜0；②9a+3b+c=0；③4ac-b²＜2a；④2b=3a．
其中正确的结论是（　　）

A．

①③

B．

②④

C．

①④

D．

②③

1．一个几何体的三视图如图所示，则这个几何体的侧面积是（　　）

A．

4π

B．

2π

C．

4

D．

π

20．一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球（除颜色外其余都相同），其中红球有2个，黑球有1个，绿球有3个，第一次任意摸出一个球（不放回），第二次再摸出一个球，则两次摸到的都是红球的概率为$\frac{1}{15}$．

19．如图，放置的△OAB₁，△B₁A₁B₂，△B₂A₂B₃，…都是边长为2的等边三角形，边AO在y轴上，点B₁，B₂，B₃，…都在直线y=$\frac{\sqrt{3}}{3}$x上，则A₂₀₁₇的坐标为（　　）

A．

2015$\sqrt{3}$，2017

B．

2016$\sqrt{3}$，2018

C．

2017$\sqrt{3}$，2019

D．

2017$\sqrt{3}$，2017

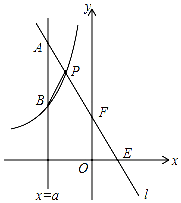18．如图，一次函数y=kx+b的图象l与坐标轴分别交于点E、F，与双曲线y=-$\frac{4}{x}$
（x＜0）交于点P（-1，n），且F是PE的中点．
（1）求直线l的解析式；
（2）若直线x=a与l交于点A，与双曲线交于点B（不同于A），
①当a为何值时，△ABP是以点P为直角顶点的直角三角形？
②当a为何值时，PA=PB．

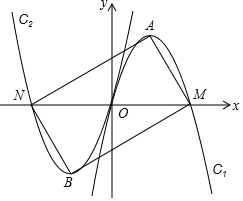17．如图，经过坐标原点的抛物线C₁：y=ax²+bx与x轴的另一交点为M，它的顶点为点A，将C₁绕原点旋转180°，得到抛物线C₂，C₂与x轴的另一交点为N，顶点为点B，连接AM，MB，BN，NA，当四边形AMBN恰好是矩形时，则b的值（　　）

A．

2$\sqrt{2}$

B．

-2$\sqrt{2}$

C．

2$\sqrt{3}$

D．

-2$\sqrt{3}$

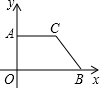16．如图，在平面直角坐标系xOy中，点A、B的坐标分别为（0，3）、（7，0），点C在第一象限，AC∥x轴，∠OBC=45°．
（1）求点C的坐标；
（2）点D在线段AC上，CD=1，点E的坐标为（n，0），在直线DE的右侧作∠DEG=45°，直线EG与直线BC相交于点F，设BF=m，当n＜7且n≠0时，求m关于n的函数解析式，并直接写出n的取值范围．