
科目: 来源: 题型:解答题
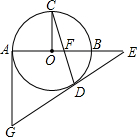 如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE=∠DFE,DE交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.
如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE=∠DFE,DE交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.查看答案和解析>>
科目: 来源: 题型:填空题
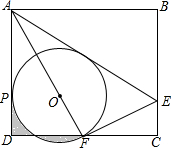 如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=3$\sqrt{3}$,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=$\frac{9}{2}$CE;④S阴影=$\frac{{\sqrt{3}}}{2}$.其中正确结论的序号是①②④.
如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=3$\sqrt{3}$,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=$\frac{9}{2}$CE;④S阴影=$\frac{{\sqrt{3}}}{2}$.其中正确结论的序号是①②④.查看答案和解析>>
科目: 来源: 题型:选择题
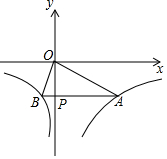 已知函数y=$\left\{\begin{array}{l}-\frac{12}{x}({x>0})\\ \frac{3}{x}({x<0})\end{array}$的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
已知函数y=$\left\{\begin{array}{l}-\frac{12}{x}({x>0})\\ \frac{3}{x}({x<0})\end{array}$的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目: 来源: 题型:选择题
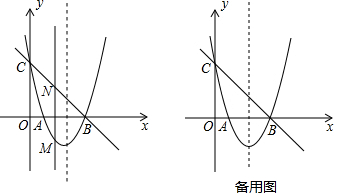
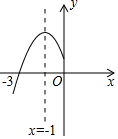 已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax-2b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象大致是( )
已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax-2b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象大致是( )| A. |  | B. | 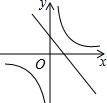 | C. |  | D. | 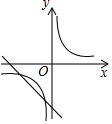 |
查看答案和解析>>
科目: 来源: 题型:解答题
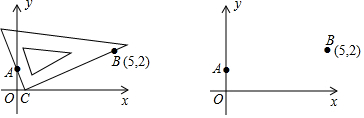
查看答案和解析>>
科目: 来源: 题型:解答题
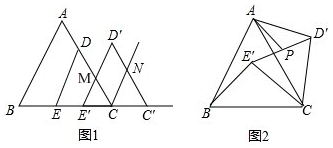
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
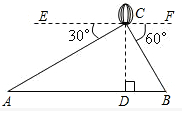 如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为120米,且点A、D、B在同一直线上,求建筑物A、B间的距离.(结果保留整数,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为120米,且点A、D、B在同一直线上,求建筑物A、B间的距离.(结果保留整数,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com