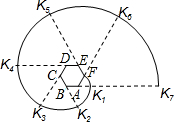15．如图，六边形ABCDEF是正六边形，曲线FK₁K₂K₃K₄K₅K₆K₇…叫做“正六边形的渐开线”，其中弧FK₁，弧K₁K₂，弧K₂K₃，弧K₃K₄，弧K₄K₅，弧K₅K₆，…的圆心依次按点A，B，C，D，E，F循环，其弧长分别记为L₁，L₂，L₃，L₄，L₅，L₆，…．当AB=1时，L₂₀₁₆等于（　　）

A．

$\frac{2016π}{2}$

B．

$\frac{2016π}{3}$

C．

$\frac{2016π}{4}$

D．

$\frac{2016π}{6}$．

14．把抛物线y=-x²向右平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（　　）

A．

y=-（x-1）2-3

B．

y=-（x+1）2-3

C．

y=-（x-1）2+3

D．

y=-（x+1）2+3

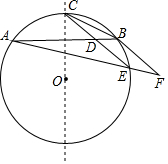13．如图示AB为⊙O的一条弦，点C为劣弧AB的中点，E为优弧AB上一点，点F在AE的延长线上，且BE=EF，线段CE交弦AB于点D．
①求证：CE∥BF；  
②若BD=2，且EA：EB：EC=3：1：$\sqrt{5}$，求△BCD的面积（注：根据圆的对称性可知OC⊥AB）．

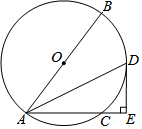12．如图，AB是⊙O的直径，C点在⊙O上，连接AC，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E．
（1）求证：DE是⊙O的切线；
（2）若AB=10，sin∠BAC=$\frac{4}{5}$，连接CD，求CD的长．

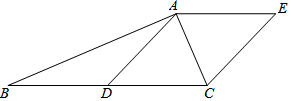11．如图，Rt△ABC中，∠BAC=90°，D是BC边的中点，连接AD，过点A作AE∥BC，且AE=CD，连接EC．
（1）求证：四边形ADCE是菱形；
（2）如果AC=a，tan∠ABC=$\frac{1}{3}$，写出求菱形ADCE的面积的思路．

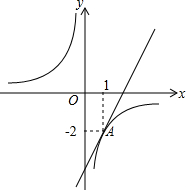10．如图，直线y=2x+b与双曲线y=$\frac{k}{x}$（k≠0）只有一个公共点A（1，-2）．
（1）求k与b的值；
（2）如果直线y=2x+m与双曲线y=$\frac{k}{x}$（k≠0）有两个公共点，请直接写出m的取值范围．

9．如图，在Rt△ABC中，∠C=90°，AB边的垂直平分线DE交BC于点E，垂足为D．
求证：∠CAB=∠AED．

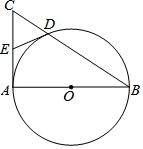8．如图，在Rt△ABC中，∠CAB=90°，以AB为直径的⊙O交BC于点D，点E是AC的中点，连接DE．
（1）求证：DE是⊙O的切线；
（2）点P是$\widehat{BD}$上一点，连接AP，DP，若BD：CD=4：1，求sin∠APD的值．

7．评价组对某区九年级教师的试卷讲评课的学生参与度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名同学的参与情况，绘制成如图所示的扇形统计图和条形统计图（均不完整），请根据图中所给信息解答下列问题：

（1）在这次评价中，一共抽查了560名同学；
（2）请将条形统计图补充完整；
（3）如果全区有6000名九年级学生，那么在试卷评讲课中，“独立思考”的约有多少人？
（4）根据统计反映的情况，请你对该区的九年级同学提出一条对待试卷讲评课的建议．

6．顺义区某中学举行春季运动会，初二年级决定从本年级300名女生中挑选64人组成花束方队，要求身高基本一致，这个工作交给年级学生会体育部小红、小冬和小芳来完成．
为了达到年级的选拔要求，小红、小冬和小芳各自对本学校初二年级的女生身高进行了抽样调查，将收集的数据进行了整理，绘制的统计表分别为表1、表2和表3．
表1 小红抽样调查初二年级4名女同学身高统计表（单位：cm）

序号	1	2	3	4
身高	155	160	165	172

表2  小冬抽样调查初二年级15名女同学身高统计表（单位：cm）

序号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
身高	148	149	150	152	152	160	160	165	166	167	168	169	170	171	175

表3 小芳抽样调查初二年级15名女同学身高统计表（单位：cm）

序号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
身高	145	160	150	152	160	154	160	166	167	168	160	169	173	174	175

根据自己的调查数据，小红说应选取身高为163cm（数据的平均数）的同学参加方队，小冬说应选取身高为165cm（数据的中位数）的同学参加方队，小芳说应选取身高为160cm（数据的众数）的同学参加方队．
根据以上材料回答问题：
小红、小冬和小芳三人中，哪一位同学的抽样调查及得出的结论更符合年级的要求，并简要说明符合要求的理由，同时其他两位同学的抽样调查或得出结论的不足之处．