8．列方程或方程组解应用题：
已知有23人在甲处劳动，17人在乙处劳动．现共调20人去支援，要使在甲处劳动的人数是在乙处劳动的人数的2倍，问应调往甲、乙两处各多少人？

7．某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
（1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；
（2）如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本=每件的成本×每天的销售量）

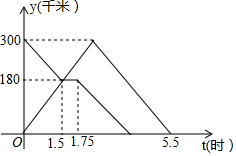6．甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地，乙车匀速前往A地，中途与甲车相遇后休息了一会儿，然后以原来的速度继续行驶直到A地．设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时）．y与x之间的函数图象如图所示，则乙车到达A地时甲车距B地的路程为150千米．

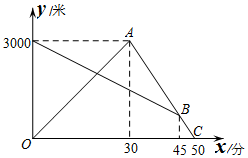5．某天早晨，小刚从家跑步去体育场锻炼，同时妈妈从体育场晨练结束回家，途中两人相遇，小刚跑到体育场后发现要下雨，立即以另一速度按原路返回，遇到妈妈后，妈妈立即以小刚返回的速度和小刚一起回家（妈妈与小刚行进的路线相同）．如图是两人离家的距离y（米）与小刚出发的时间x（分）之间的函数图象，则小刚第一次和妈妈相遇时，妈妈离家的距离为2000 米．

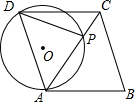4．如图，点P在菱形ABCD的对角线AC上，PA=PD，⊙O为△APD的外接圆．
（1）求证：△APD∽△ADC．
（2）若AD=6，AC=8，求⊙O的半径．

3．现有一个圆心角为90°，半径为12cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），该圆锥底面圆的半径为3cm．

2．因式分解：9x²-9=9（x+1）（x-1）．

1．若实数a、b满足（a+b）（a+b-6）+9=0，则a+b的值为3．

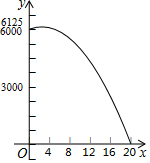20．某商品的进价为每件40元，当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查，每降价1元，每星期可多卖出20件，在确保盈利的前提下，解答下列问题：
（1）若设每件降价x（x为整数）元，每星期售出商品的利润为y元，请写出x与y之间的函数关系式，并求出自变量x的取值范围；
（2）请画出上述函数的大致图象．
（3）当降价多少元时，每星期的利润最大？最大利润是多少？
小丽解答过程如下：
解：（1）根据题意，可列出表达式：
y=（60-x）（300+20x）-40（300+20x），
即y=-20x²+100x+6000．
∵降价要确保盈利，∴40＜60-x≤60．解得0≤x＜20．
（2）上述表达式的图象是抛物线的一部分，函数的大致图象如图1：
（3）∵a=-20＜0，
∴当x=-$\frac{b}{2a}$=2.5时，y有最大值，y=$\frac{4ac-{b}^{2}}{4a}$=6125．
所以，当降价2.5元时，每星期的利润最大，最大利润为6125．
老师看了小丽的解题过程，说小马第（1）问的表达式是正确的，但自变量x的取值范围不准确．（2）（3）问的答案，也都存在问题．请你就老师说的问题，进行探究，写出你认为（1）（2）（3）中正确的答案，或说明错误原因．

19．解方程：$\frac{3}{x-2}$-$\frac{1}{x}$=$\frac{3}{{x}^{2}-2x}$．