科目： 来源： 题型：解答题

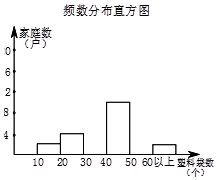8．小明要统计小区500户居民每月丢弃塑料袋的数量情况，他随机调查了其中40户居民，按每月丢弃的塑料袋的数量分组进行统计，并绘制了如下的频数分布表和频数分布直方图：

组别	每月丢塑料袋个数	频数	频率
第1组	10至19	2	0.05
第2组	20至29	4	0.10
第3组	30至39	6	0.15
第4组	40至49	10	0.25
第5组	50至59	16	0.40
第6组	60以上	2	0.05
	合计	40	1.00

根据以上提供的信息，解答下列问题：
（1）补全频数分布表和频数分布直方图；
（2）请你估算该小区每月丢弃塑料袋的数不少于40个的户数大约有多少户？

科目： 来源： 题型：解答题

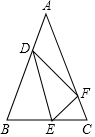7．如图，在△ABC中，AB=AC，点E在边BC上移动（点E不与点B，C重合），满足∠DEF=∠B，且点D、F分别在边AB、AC上．
（1）求证：△BDE∽△CEF；
（2）当点E移动到BC的中点时，求证：FE平分∠DFC．

科目： 来源： 题型：填空题

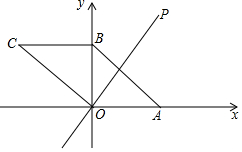6．如图，在平面直角坐标系xOy中，?ABCO的顶点A，B的坐标分别是A（3，0），B（0，2）．动点P在直线y=$\frac{3}{2}$x上运动，以点P为圆心，PB长为半径的⊙P随点P运动，当⊙P与?ABCO的边相切时，P点的坐标为（0，0）或（$\frac{2}{3}$，1）或（3-$\sqrt{5}$，$\frac{9-3\sqrt{5}}{2}$）．

科目： 来源： 题型：解答题

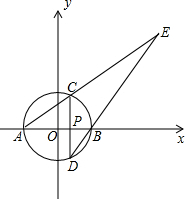5．如图，以原点O为圆心，3为半径的圆与x轴分别交于A，B两点（点B在点A的右边），P是半径OB上一点，过P且垂直于AB的直线与⊙O分别交于C，D两点（点C在点D的上方），直线AC，DB交于点E．若AC：CE=1：2．
（1）求点P的坐标；
（2）求过点A和点E，且顶点在直线CD上的抛物线的函数表达式．

科目： 来源： 题型：填空题

科目： 来源： 题型：选择题

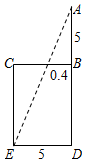3．“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为（　　）

A．

1.25尺

B．

57.5尺

C．

6.25尺

D．

56.5尺

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

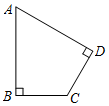1．已知：如图，四边形ABCD中，∠ABC=∠ADC=90°，AB=AD．
（1）求证：BC=CD；
（2）若∠A=60°，将线段BC绕着点B逆时针旋转60°，得到线段BE，连接DE，在图中补全图形，并证明四边形BCDE是菱形．

科目： 来源： 题型：解答题

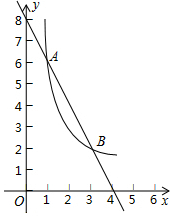20．如图，一次函数y=kx+b（k≠0）与反比例函数y=$\frac{m}{x}$（m≠0）的图象在第一象限内交于A（1，6），B（3，n）两点．
（1）求这两个函数的表达式；
（2）根据图象直接写出kx+b-$\frac{m}{x}$＜0的x的取值范围．

科目： 来源： 题型：解答题

19．如图，AB为⊙O的直径，直线CD切⊙O于点M，BE⊥CD于点E．
（1）求证：∠BME=∠MAB；
（2）如果BE=$\frac{18}{5}$，sin∠BAM=$\frac{3}{5}$，求⊙O的半径．