科目： 来源： 题型：选择题

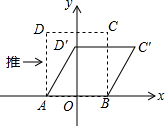10．我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为（　　）

A．

（$\sqrt{3}$，1）

B．

（2，1）

C．

（1，$\sqrt{3}$）

D．

（2，$\sqrt{3}$）

科目： 来源： 题型：解答题

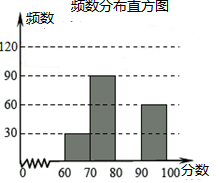9．某校举行了”文明河南中小学生知识竞赛“活动，并随即抽查了部分同学的成绩，整理并制作成图表如下：

分数段	频数	频率
60≤x＜70	30	0.1
70≤x＜80	90	n
80≤x＜90	m	0.4
90≤x≤100	60	0.2

请根据以上图表提供的信息，解答下列问题：
（1）请求出：m=120，n=0.3，抽查的总人数为300人；
（2）请补全频数分布直方图；
（3）抽查成绩的中位数应落在80≤x＜90分数段内；
（4）如果比赛成绩在80分以上（含80分）为优秀，任意抽取一位同学，则成绩优秀的概率为多少？

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

4．已知在平面直角坐标系xOy中（如图），已知抛物线y=-x²+bx+c经过点A（2，2），对称轴是直线x=1，顶点为B．
（1）求这条抛物线的表达式和点B的坐标；
（2）点M在对称轴上，且位于顶点上方，设它的纵坐标为m，联结AM，用含m的代数式表示∠AMB的余切值；
（3）将该抛物线向上或向下平移，使得新抛物线的顶点C在x轴上．原抛物线上一点P平移后的对应点为点Q，如果OP=OQ，求点Q的坐标．

科目： 来源： 题型：填空题

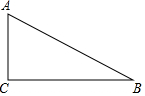3．如图，已知Rt△ABC，∠C=90°，AC=3，BC=4．分别以点A、B为圆心画圆．如果点C在⊙A内，点B在⊙A外，且⊙B与⊙A内切，那么⊙B的半径长r的取值范围是8＜r＜10．

科目： 来源： 题型：解答题

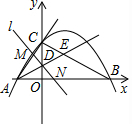2．如图，已知抛物线y=ax²-2$\sqrt{3}$ax-9a与坐标轴交于A，B，C三点，其中C（0，3），∠BAC的平分线AE交y轴于点D，交BC于点E，过点D的直线l与射线AC，AB分别交于点M，N．
（1）直接写出a的值、点A的坐标及抛物线的对称轴；
（2）点P为抛物线的对称轴上一动点，若△PAD为等腰三角形，求出点P的坐标；
（3）证明：当直线l绕点D旋转时，$\frac{1}{AM}$+$\frac{1}{AN}$均为定值，并求出该定值．

科目： 来源： 题型：解答题

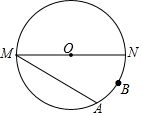1．如图，MN是⊙O的直径，MN=4，点A在⊙O上，∠AMN=30°，B为$\widehat{AN}$的中点，P是直径MN上一动点．
（1）利用尺规作图，确定当PA+PB最小时P点的位置（不写作法，但要保留作图痕迹）．
（2）求PA+PB的最小值．