
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
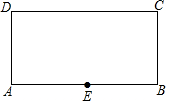 如图,点E为矩形ABCD边AB的中点,连接CE,作射线DE,若点F为矩形ABCD边上任意一点,沿EF将矩形折叠,使点A恰好落在射线DE上,已知AD=2,CD=4.则DF=4-2$\sqrt{2}$或3$\sqrt{2}$.
如图,点E为矩形ABCD边AB的中点,连接CE,作射线DE,若点F为矩形ABCD边上任意一点,沿EF将矩形折叠,使点A恰好落在射线DE上,已知AD=2,CD=4.则DF=4-2$\sqrt{2}$或3$\sqrt{2}$.查看答案和解析>>
科目: 来源: 题型:解答题
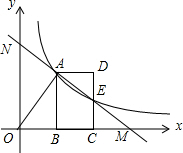 如图,反比例函数y=$\frac{m}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
如图,反比例函数y=$\frac{m}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.查看答案和解析>>
科目: 来源: 题型:选择题
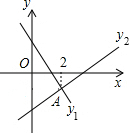 如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )
如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )| A. | k>0 | B. | m>n | C. | 当x<2时,y2>y1 | D. | 2k+n=m-2 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
| x | … | -2 | -1 | 0 | 1 | 1.4 | 2.4 | 2.5 | 3 | 4 | 5 | … |
| y | … | -3.25 | -2.33 | -1.50 | -1 | -1.27 | 3.9 | 3.5 | 3 | m | 4.33 | … |
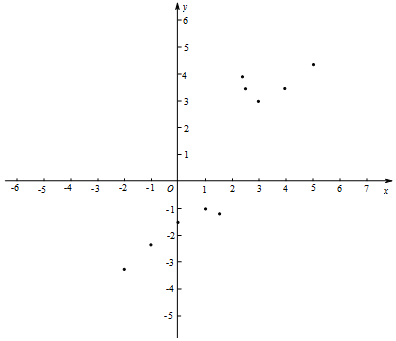
查看答案和解析>>
科目: 来源: 题型:选择题
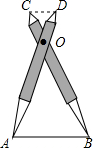 如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使OA=4OD,OB=4OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若CD=3,则AB的长是( )
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使OA=4OD,OB=4OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若CD=3,则AB的长是( )| A. | 12 | B. | 9 | C. | 8 | D. | 6 |
查看答案和解析>>
科目: 来源: 题型:解答题
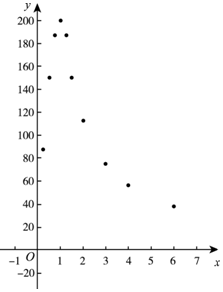 阅读下列材料:
阅读下列材料:| 饮酒后的时间x (小时) | … | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{3}{4}$ | 1 | $\frac{5}{4}$ | $\frac{3}{2}$ | 2 | 3 | 4 | 5 | 6 | … |
| 血液中酒精含量y (毫克/百毫升) | … | $\frac{175}{2}$ | 150 | $\frac{375}{2}$ | 200 | $\frac{375}{2}$ | 150 | $\frac{225}{2}$ | $\frac{225}{3}$ | $\frac{225}{4}$ | 45 | $\frac{225}{6}$ | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com