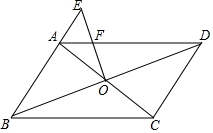11．如图，在?ABCD中，对角线AC、BD相交于点O，在BA的延长线上取一点E，连接OE交AD于点F．若CD=5，BC=8，AE=2，则AF=$\frac{16}{9}$．

10．定义：A={b，c，a}，B={c}，A∪B={a，b，c}，若M={-1}，N={0，1，-1}，则M∪N={1，0，-1}．

9．三角形的两边a、b的夹角为60°且满足方程x²-3$\sqrt{2}$x+4=0，则第三边的长是（　　）

A．

$\sqrt{6}$

B．

2$\sqrt{2}$

C．

2$\sqrt{3}$

D．

3$\sqrt{2}$

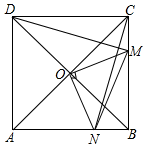8．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN²+CM²=MN²；⑤若AB=2，则S_△OMN的最小值是$\frac{1}{2}$，其中正确结论的个数是（　　）

A．

2

B．

3

C．

4

D．

5

7．已知函数y=4x²-4（m+3）x+m²+6m，求证函数图象与x轴恒有两个交点A，B，并求|AB|的值．

6．为确保广大居民家庭基本用水需求的同时鼓励家庭节约用水，对居民家庭每户每月用水量采用分档递增收费的方式，每户每月用水量不超过基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费．为对基本用水量进行决策，随机抽查2000户居民家庭每户每月用水量的数据，整理绘制出下面的统计表：

用户每月用水量（m3）	32及其以下	33	34	35	36	37	38	39	40	41	42	43及其以上
户数（户）	200	160	180	220	240	210	190	100	170	120	100	110

（1）为确保70%的居民家庭每户每月的基本用水量需求，那么每户每月的基本用水量最低应确定为多少立方米？
（2）若将（1）中确定的基本用水量及其以内的部分按每立方米1.8元交费，超过基本用水量的部分按每立方米2.5元交费．设x表示每户每月用水量（单位：m³），y表示每户每月应交水费（单位：元），求y与x的函数关系式；
（3）某户家庭每月交水费是80.9元，请按以上收费方式计算该家庭当月用水量是多少立方米？

5．如图，点 A，B，C均在6×6的正方形网格格点上，过A，B，C三点的外接圆除经过A，B，C三点外还能经过的格点数为5．

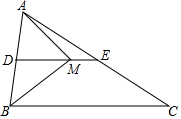4．在△ABC中，AB=6，点D是AB的中点，过点D作DE∥BC，交AC于点E，点M在DE上，且ME=$\frac{1}{3}$DM．当AM⊥BM时，则BC的长为8．

3．如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是（　　）

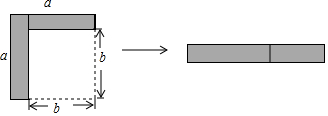
A．

（a-b）2=a2-2ab+b2

B．

a（a-b）=a2-ab

C．

（a-b）2=a2-b2

D．

a2-b2=（a+b）（a-b）

2．星期日，小英与小平同时从家里出发返回学校，速度分别为3千米/小时，4千米/小时，小平家离学校18千米，小英家在小平返校的路上，离小平家2千米．
（1）分别写出小英、小平离小平家的距离y（千米）与行走时间t（小时）的函数关系式；
（2）在同一直角坐标系中画出上述两个函数的图象；
（3）返校路上，小平能否追上小英？如能，出发后几小时追上？
（4）从图象上看：谁先到达学校？