7．已知x+$\frac{1}{x}$=3，则下列三个等式：①x²+$\frac{1}{x^2}$=7，②x-$\frac{1}{x}=\sqrt{5}$，③2x²-6x=-2中，正确的个数有（　　）

A．

0个

B．

1个

C．

2个

D．

3个

6．如图是“明清影视城”的一扇圆弧形门，小红到影视城游玩，他了解到这扇门的相关数据：这扇圆弧形门所在的圆与水平地面是相切的，AB=CD=0.25米，BD=1.5米，且AB、CD与水平地面都是垂直的．根据以上数据，请你帮小红计算出这扇圆弧形门的最高点离地面的距离是（　　）

A．

2米

B．

2.5米

C．

2.4米

D．

2.1米

5．已知关于x，y的方程组$\left\{\begin{array}{l}{x-2y=m①}\\{2x+3y=2m+4②}\end{array}\right.$的解满足不等式组$\left\{\begin{array}{l}{3x+y≤0}\\{x+5y＞0}\end{array}\right.$，求满足条件的m的整数值．

4．解不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1①}\\{1-3（x-1）＜10-x②}\end{array}\right.$，并把解集在数轴上表示出来．

3．如图，已知EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD的度数，下面给出了求∠AGD的度数的过程，将此补充完整并在括号里填写依据．
【解】∵EF∥AD（已知）
∴∠2=∠3（两直线平行，同位角相等）
又∵∠1=∠2（已知）
∴∠1=∠3（等式性质或等量代换）
∴AB∥DG（内错角相等，两直线平行）
∴∠BAC+∠AGD=180°（两直线平行，同旁内角互补）
又∵∠BAC=70°（已知）
∴∠AGD=110°（等式性质）

2．解方程组：$\left\{\begin{array}{l}{3x+2y=5①}\\{2x+5y=7②}\end{array}\right.$．

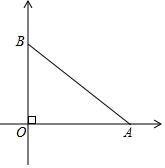1．甲、乙两位探险者今年到沙漠进行探险，没有了水，需要寻找水源，为了不致于走散，他们用两部对话机联系，已知对话机的有效距离为12千米，早晨8：00甲先出发，他以4千米/时的速度向东行走，1小时后乙出发，他以6千米/时的速度向北行进，上午10：00，甲、乙二人相距多远？还能保持联系吗？

20．手机党，简称MP，是对使用手机进行互联网交流人群的称谓．他们做任何事都离不开手机，有些甚至过分依赖手机而形成了“手机瘾”．某校团组织为了解初三毕业生的手机使用情况，随机调查了部分初三毕业生的手机使用时间，并将调查结果分成了以下五类（每类仅包含最大数值）：A、基本不用；B、平均每天使用1～2小时；C、平均每天使用2～4小时；D、平均每天使用4～6小时；E、平均每天使用超过6小时．且绘制了如下两幅统计图（部分信息未给全）．
（1）求本次共调查的学生人数，并补全条形统计图；
（2）已知该校2017年初三毕业生共900人，若平均每天使用手机的时间超过4小时，则患有严重“手机瘾”，试估计该校初三毕业生中患有严重“手机瘾”的学生人数；
（3）根据统计图提供的信息，谈谈你的看法（不超过30字）．

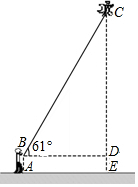19．小蓝周末去广场放风筝，如图，当风筝飞到点C处时的线长BC约为25m，此时小蓝正好站在点A处，并测得∠CBD=61°，牵引底端B距离地面1.5m，则此时风筝距离地面的高度CE约为23.3m（用科学计算器计算，结果精确到0.1m）．

18．阅读理解：
已知直线l₁的函数表达式为y=k₁x+b₁（k₁≠0，k₁，b₁为常数），直线l₂的函数表达式为y=k₂x+b₂（k₂≠0，k₂，b₂为常数），若l₁⊥l₂，则有k₁•k₂=-1．
问题解决：
（1）已知直线y=4x+1与直线y=kx-1垂直，求k的值；
（2）若直线l经过A（-2，-5），且与y=-$\frac{1}{3}$x+3垂直，求直线l的表达式．