
科目: 来源:2017届广东省梅州市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
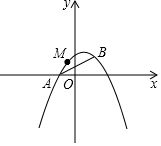 如图,已知抛物线y=ax2+bx+1经过A(-1,0),B(1,1)两点.
如图,已知抛物线y=ax2+bx+1经过A(-1,0),B(1,1)两点.查看答案和解析>>
科目: 来源: 题型:解答题
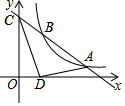 如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(4,n)和点$B(n+\frac{1}{3},3)$,与y轴交于点C.
如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(4,n)和点$B(n+\frac{1}{3},3)$,与y轴交于点C.查看答案和解析>>
科目: 来源: 题型:解答题
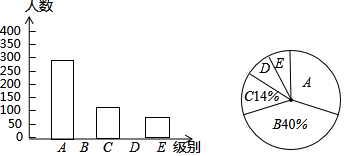 某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.
某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.| 组别 | 获取新闻的最主要途径 | 人数 |
| A | 电脑上网 | 280 |
| B | 手机上网 | m |
| C | 电视 | 140 |
| D | 报纸 | n |
| E | 其它 | 80 |
查看答案和解析>>
科目: 来源: 题型:填空题
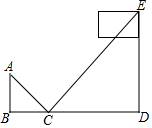 处看到旗杆顶部E,此时小军的站立点B与点C的水平距离为2m,旗杆底部D与点C的水平距离为12m.若小军的眼睛距离地面的高度为1.5m(即AB=1.5m),则旗杆的高度为9m.
处看到旗杆顶部E,此时小军的站立点B与点C的水平距离为2m,旗杆底部D与点C的水平距离为12m.若小军的眼睛距离地面的高度为1.5m(即AB=1.5m),则旗杆的高度为9m.查看答案和解析>>
科目: 来源:2017届广东省梅州市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.
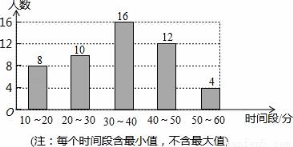
(1)求样本容量,并估计全校同学在周末期间平均每夭做家务活的时间在40分钟以上(含40分钟)的人数;
(2)校学生会拟在表现突出的A、B、C、D四名同学中,随机抽取两名同学向全校汇报.请用树状图或列表法表示出所有可能的结果,并求恰好抽到A、B两名同学的概率.
查看答案和解析>>
科目: 来源: 题型:选择题
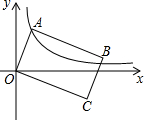 如图,已知点A是反比例函数y=$\frac{{\sqrt{6}}}{x}$在第一象限图象上的一个动点,连接OA,以$\sqrt{3}$OA为长,OA为宽作矩形AOCB,且点C在第四象限,随着点A的运动,点C也随之运动,但点C始终在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,已知点A是反比例函数y=$\frac{{\sqrt{6}}}{x}$在第一象限图象上的一个动点,连接OA,以$\sqrt{3}$OA为长,OA为宽作矩形AOCB,且点C在第四象限,随着点A的运动,点C也随之运动,但点C始终在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -3$\sqrt{6}$ | B. | 3$\sqrt{6}$ | C. | -$\sqrt{6}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com