
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
| 上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 本年度保险费(元) | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
| 出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 频数 | 30 | 30 | m | 15 | 10 | 5 |
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,AB为⊙O的直径,点P是⊙O外一点,PD与⊙O相切于点C,与BA的延长线交于点D,DE⊥PO,交PO的延长线于点E,连接PB,∠EDB=∠EPB.
如图,AB为⊙O的直径,点P是⊙O外一点,PD与⊙O相切于点C,与BA的延长线交于点D,DE⊥PO,交PO的延长线于点E,连接PB,∠EDB=∠EPB.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
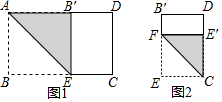 矩形纸片ABCD中,AD=10,AB=a(5<a<10)
矩形纸片ABCD中,AD=10,AB=a(5<a<10)查看答案和解析>>
科目: 来源: 题型:解答题
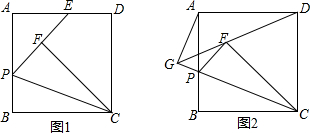
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
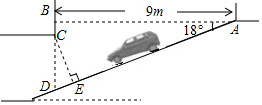 为缓解“停车难”的问题,某单位拟造地下停车库,建筑设计师提供了该地下停车库的设计示意图如图所示,已知该坡道的水平距离AB的长为9m,坡面AD与AB的夹角∠BAD=18°,石柱BC=0.5m,按规定,地下停车库坡道上方BC处要张贴限高标志,以便告知停车人车辆能否安全驶入.请你帮设计师计算一下CE的高度,以便张贴限高标志,结果精确到0.1m.
为缓解“停车难”的问题,某单位拟造地下停车库,建筑设计师提供了该地下停车库的设计示意图如图所示,已知该坡道的水平距离AB的长为9m,坡面AD与AB的夹角∠BAD=18°,石柱BC=0.5m,按规定,地下停车库坡道上方BC处要张贴限高标志,以便告知停车人车辆能否安全驶入.请你帮设计师计算一下CE的高度,以便张贴限高标志,结果精确到0.1m.查看答案和解析>>
科目: 来源: 题型:解答题
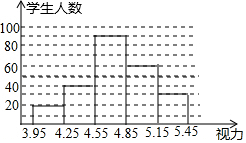 近年来“低头族”现象日趋严重,初中生的视力状况受到了全社会的广泛关注.某市有关部门对全市3万名初中生视力状况进行了一次抽样调查,并利用所得的数据绘制了如图的频数分布直方图,根据图中提供的信息解答下列问题:
近年来“低头族”现象日趋严重,初中生的视力状况受到了全社会的广泛关注.某市有关部门对全市3万名初中生视力状况进行了一次抽样调查,并利用所得的数据绘制了如图的频数分布直方图,根据图中提供的信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com