19．如图1，在平面直角坐标系中，抛物线y=-$\frac{\sqrt{3}}{2}$x²+$\frac{3\sqrt{3}}{2}$x+2$\sqrt{3}$与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．
（1）求直线BC的解析式；
（2）点D是线段BC中点，点E是BC上方抛物线上一动点，连接CE，DE．当△CDE的面积最大时，过点E作y轴垂线，垂足为F，点P为线段EF上一动点，将△CEF绕点C沿顺时针方向旋转90°，点F，P，E的对应点分别是F′，P′，E′，点Q从点P出发，先沿适当的路径运动到点F′处，再沿F′C运动到点C处，最后沿适当的路径运动到点P′处停止．求△CDE面积的最大值及点Q经过的最短路径的长；
（3）如图2，直线BH经过点B与y轴交于点H（0，3）动点M从O出发沿OB方向以每秒1个单位长度向点B运动，同时动点N从B点沿BH方向以每秒2个单位长度的速度向点H运动，当点N运动到H点时，点M，点N同时停止运动，设运动时间为t．运动过程中，过点N作OB的平行线交y轴于点I，连接MI，MN，将△MNI沿NI翻折得△M′NI，连接HM′，当△M′HN为等腰三角形时，求t的值．

18．如图，?ABCD的对角线AC、BD相交于点O，若AB=5cm，BC=7cm，△COD的周长是17cm，则△BOC的周长是19cm．

17．若a+b=5，ab=2，则a²+b²=21．

16．已知：如图，直线y=-x+m分别与x轴交于点A（6，0），y轴交于点B，抛物线y=-x²+bx+c经过点A，B．
（1）求m的值和抛物线的解析式．
（2）若点P从点O向点A以每秒2个单位长度运动，设运动时间t（0＜t＜3）．
①若过点P作PM垂直x轴，交抛物线于点M，AB于点N，设点M，N两点之间的距离为s．请你用含t的代数式表示s，并求出当s取最大值时t的值．
②若点Q也同时从点B向点O以每秒3个单位长度运动，当运动到点O时点P、点Q都停止运动．连结BP、AQ，且交于点C，当∠ACP=45°时，求t的值．

15．将下列多项式因式分解，结果中不含有因式a+1的是（　　）

A．

a2-1

B．

a2+a

C．

（a-1）2-a+1

D．

（a+2）2-2（a+2）+1

14．如图，四边形ABCD是正方形，AE垂直于BE，且AE=6，BE=8，则阴影部分的面积是（　　）

A．

66

B．

76

C．

64

D．

100

13．一组数据1，3，2，5，2，a的众数是a，这组数据的中位数是（　　）

A．

3

B．

2

C．

1.5

D．

2.5

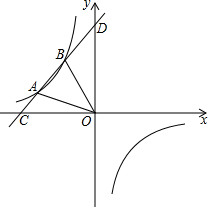12．如图，直线y=mx+n（m≠0）与双曲线y=$\frac{k}{x}$（k≠0）交于A、B两点，直线AB与坐标轴分别交于C、D两点，连接OA，若OA=2$\sqrt{10}$，tan∠AOC=$\frac{1}{3}$，点B（-3，b）．
（1）分别求出直线AB与双曲线的解析式；
（2）连接OB，求S_△AOB．

11．解方程组
（1）$\left\{\begin{array}{l}{x+y=1}\\{2x-y=-4}\end{array}\right.$                    
（2）$\left\{\begin{array}{l}{3（x-1）=4（y-4）}\\{5（y-1）=3（x+5）}\end{array}\right.$．

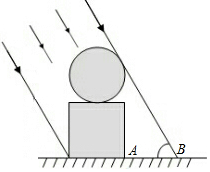10．如图，广场上一个立体雕塑由两部分组成，底座是一个正方体，正上方是一个球体，且正方体的高度和球的高度相等．当阳光与地面的夹角成60°时，整个雕塑在地面上的影子AB长2米，求这个雕塑的高度．（结果精确到百分位，参考数据：$\sqrt{3}$≈1.73）