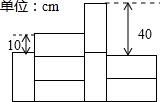2．如图是由同一种长方形的墙砖粘贴的部分墙面，其中3块横放的墙砖比1块竖放的墙砖高10cm，2块横放的墙砖比2块竖放的墙砖低40cm，则每块墙砖的面积是（　　）

A．

425cm2

B．

525cm2

C．

600cm2

D．

800cm2

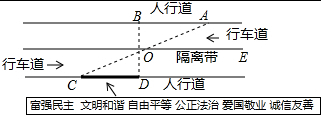1．小明沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙0点，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息如下：如图，AB∥OE，OE∥CD，AC与BD相交于点O，OD⊥CD，垂足为点D，下列结论中不正确的是（　　）

	A．	∠BOA=∠DOC		B．	AB∥CD
	C．	∠ABD=90°		D．	与∠AOE相等的角共有2个

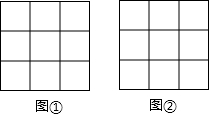20．在边长为1个单位长度的小正方形组成的3×3的正方形网格图①、图②中，各画一个顶点在格点上的平行四边形，要求：每个平行四边形均为轴对称图形，每个平行四边形至少有一条边长为$\sqrt{5}$，所画的两个四边形不全等．

19．问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC度数．
小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC=50°+60°=110°．
问题迁移：
（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；
（2）在（1）的条件下，如果点P在A、M两点之间和B、O两点之间上运动时（点P与点A、B、O三点不重合），请你分别直接写出∠CPD、∠α、∠β间的数量关系．

18．计算：（-2）²⁰¹⁶+（-2）²⁰¹⁷所得的结果是（　　）

A．

-2

B．

2

C．

-22016

D．

22016

17．利用勾股定理可以在数轴上画出表示$\sqrt{20}$的点，请依据以下思路完成画图，并保留画图痕迹：
第一步：（计算）尝试满足$\sqrt{20}$=$\sqrt{{a}^{2}+{b}^{2}}$，使其中a，b都为正整数，你取的正整数a=4，b=2；
第二步：（画长为$\sqrt{20}$的线段）以第一步中你所取的正整数a，b为两条直角边长画Rt△OEF，使O为原点，点E落在数轴的正半轴上，∠OEF=90°，则斜边OF的长即为$\sqrt{20}$，请在下面的数轴上画图；（第二步不要求尺规作图，不要求写画法）
第三步：（画表示$\sqrt{20}$的点）在下面的数轴上画出表示$\sqrt{20}$的点M，并描述第三步的画图步骤：以原点为圆心，OF为半径画弧交数轴的正半轴于点M，则点M为所作．

16．计算：
（1）$\frac{1}{2}\sqrt{12}$-（3$\sqrt{\frac{1}{3}}$+$\sqrt{5}}$）
（2）2017⁰+$\sqrt{8}$+2×2^-1-|$\sqrt{2}$-2|．

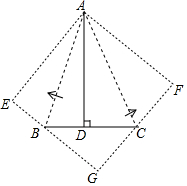15．如图，△ABC中，∠BAC=45°，AD⊥BC于D，BD=3，AD=8，求DC的长．
小萍同学灵活运用轴对称知识，将图形进行翻折变换，巧妙地解答了此题．
请按照小萍的思路，探究并解答下列问题：
（1）分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点为E、F，延长EB、FC相交于G点，证明四边形AEGF是正方形；
（2）设DC=x，利用勾股定理，建立关于x的方程模型，求出x的值．

14．计算：
（1）（-1）²⁰¹⁶-（-3）+（7-π）⁰+（-$\frac{1}{2}$）^-1；
（2）（m¹²÷m⁹）•m²+（m²）⁴÷m²．

13．已知：M（4，4），N（-2，-2），在横轴上存在点P，使PM=PN．求点P的坐标．