科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

11．如图，按要求作图：
（1）过点P作直线CD平行于AB；
（2）过点P作PE⊥AB，垂足为O．

科目： 来源： 题型：解答题

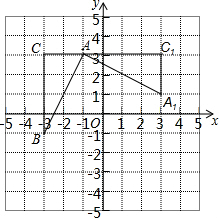10．如图，在平面直角坐标系中，有一Rt△ABC，且点A（-1，3），B（-3，-1），C（-3，3），已知△A₁AC₁是由△ABC旋转得到的．
（1）旋转中心的坐标是O（0，0），旋转角的度数是90°．
（2）以（1）中的旋转中心为中心，分别画出△A₁AC₁顺时针旋转90°，180°的三角形．
（3）利用变换前后所形成的图案，可以证明的定理是勾股定理．

科目： 来源： 题型：解答题

9．宽与长的比是$\frac{\sqrt{5}-1}{2}$的矩形叫做黄金矩形．黄金矩形给我们以协调、匀称的美感．世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计．请用尺规作图的方法在方格纸中作出一个黄金矩形（自己确定边的长度）

科目： 来源： 题型：解答题

科目： 来源： 题型：选择题

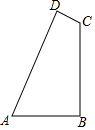7．如图，在四边形ABCD中，AB=3，BC=4，CD=1，AD=2$\sqrt{6}$，AB⊥BC，四边形ABCD的面积为（　　）

A．

12

B．

6+$\sqrt{6}$

C．

2$\sqrt{6}$

D．

2$\sqrt{6}$+6

科目： 来源： 题型：解答题

6．如图，在△ABC中，D是边BC上一点，若AB=10，BD=6，AD=8，AC=17，求BC的长．

科目： 来源： 题型：解答题

5．（1）如图1，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A=30°，求∠D的度数．

（2）如图2，E，C在BF上，AB=DE，AC=DF，BE=CF，试说明：AC∥DF．

科目： 来源： 题型：解答题

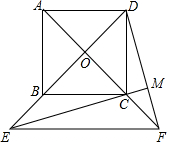4．如图，正方形ABCD的对角线AC、BD相交于点O，点E在DB的延长线上，连接EC．过点D作DM⊥EC，垂足为M，DM与AC相交于点F，连接EF．求证：
EF∥BC．

科目： 来源： 题型：解答题

3．阅读下面材料：小明遇到这样一个问题：如图1，在△ABC中，DE∥BC分别交AB于D，交AC于E，已知CD⊥BE，CD=2，BE=3，求BC+DE的值．
小明发现，过点E作EF∥DC，交BC延长线于点F，构造△BEF，经过推理和计算能够使问题得到解决（如图2）．
（1）请按照上述思路完成小明遇到的这个问题．
（2）参考小明思考问题的方法，解决问题：
如图3，已知?ABCD和矩形ABEF，AC与DF交于点G，AC=BF=DF，求∠DGC的度数．