
科目: 来源: 题型:解答题
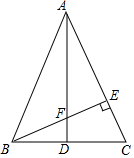 如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?
如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?查看答案和解析>>
科目: 来源: 题型:解答题
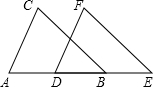 把下面的推理过程补充完整,并在括号内注明理由
把下面的推理过程补充完整,并在括号内注明理由查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
| 汽车行驶时间t(h) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
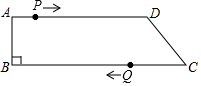 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
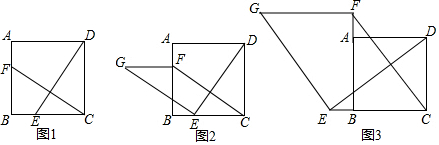
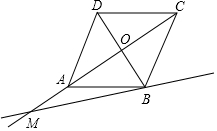 如图,O为菱形ABCD对角线的交点,M是射线CA上的一个动点(点M与点C,O,A都不重合),过点A,C分别向直线BM作垂线段,垂足分别为E,F,连接OE,OF.
如图,O为菱形ABCD对角线的交点,M是射线CA上的一个动点(点M与点C,O,A都不重合),过点A,C分别向直线BM作垂线段,垂足分别为E,F,连接OE,OF.查看答案和解析>>
科目: 来源: 题型:解答题
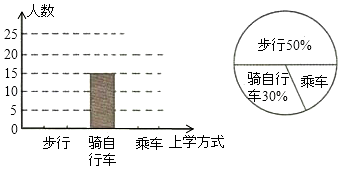
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com