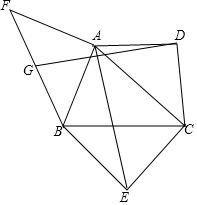19．如图所示，已知△ABC是锐角三角形，以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE，以边AB为直角边向形外作等腰直角三角形ABF，∠BAF=90°，点G为BF的中点，连接GD和AE，试探究GD和AE的数量关系和位置关系，并对你的结论加以证明．

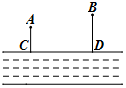18．如图，某河的同侧有A，B两个工厂，它们垂直于河边的小路的长度分别为AC=2km，BD=3km，这两条小路相距5km．现要在河边建立一个抽水站，把水送到A，B两个工厂去，若使供水管最短，抽水站应建立的位置为（　　）

A．

距C点1km处

B．

距C点2km处

C．

距C点3km处

D．

CD的中点处

17．已知△ABC的三边a=m-n（m＞n＞0），b=m+n，c=2$\sqrt{mn}$．
（1）求证：△ABC是直角三角形；
（2）利用第（1）题的结论，写出两组m，n的值，要求三角形的边长均为整数．

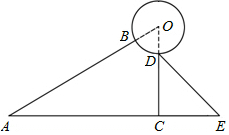16．如图是某品牌太阳能热水器的实物图和横断面示意图，已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心O，支架CD与水平面AE垂直，AB=150厘米，∠BAC=30°，另一根辅助支架DE=40$\sqrt{3}$厘米，∠CED=60°．
（1）求垂直支架CD的长度；
（2）求水箱半径OD的长度．

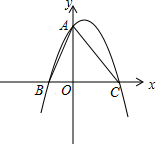15．如图，在平面直角坐标系中，二次函数y=-x²+x+6的图象与y轴交于点A，与x轴交于B，C两点（点B在点C的左侧），连接AB，AC．
（1）①点B的坐标为（-2，0），点C的坐标为（3，0），AC的长为3$\sqrt{5}$；
②求∠BAC的正弦值
（2）将△AOB沿直线AB折叠得到△AEB，将△AOC沿直线AC折叠得到△AFC，分别延长EB，FC相交于点H
①点H坐标为（$\frac{6}{5}$，-$\frac{12}{5}$），点H不在抛物线对称轴上（“在”或“不在”）
②连接EF，将∠BAC绕点A顺时针旋转，射线AB旋转后交线段EH于点B′，交线段EF于点M，射线AC旋转后交线段FH于点C′，交线段EF于点N，当B′H²+C′H²=33时，MN的长度为$\frac{\sqrt{66}}{2}$．

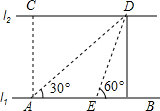14．如图，河的两岸l₁与l₂互相平行，A、B是l₁上的两点，C、D是l₂上的两点，某同学在A处测得∠CAB=90°，∠DAB=30°，再沿AB方向走20米到达点E（即AE=20），测得∠DEB=60°．
求：C，D两点间的距离．

13．根据下列问题，列出关于x的方程，并将其化为一般形式．
（1）正方体的表面积是36，求正方体的边长x；
（2）小明用30厘米的铁丝围成一斜边长等于13厘米的直角三角形，该直角三角形的一直角边长x厘米，求该直角三角形的两直角边．

12．老师让同学们回家准备一根21cm长的细木棒留着课堂上用，小明为了防止木棒折断，想把它放入自己的文具盒中，已知小明的文具盒是一个长20cm，宽8cm的长方体（高与细木棒粗细一致），请问小明准备的木棒能放进他的文具盒吗？

11．我国古代数学著作《九章算术》中有这样一个问题：今有池方一丈，葭生其中央，出水一尺．引葭赴岸，适于岸齐，问水深、葭长各几何？”这道题的意思是说：“有一个边长为10尺的正方形水池，在水池的正中央长着一根芦苇，芦苇露出水面1尺，若将芦苇拉到水池一边的中点处，芦苇的顶端恰好到达池边的水面，问水的深度与这根芦苇的长度分别是多少？若设水的深度为x尺，则可以得到方程x²+5²=（x+1）²．

10．如图1，抛物线y=ax²+bx+c（a＞0）与y轴正半轴交于C点，与x轴正半轴交于A，B两点，其中点A在点B左边，D为抛物线的顶点，连AC、BC、AD、BD
（1）若a=1，且∠ACO=∠OBC，求c的值；
（2）∠ADB=120°，求b²-4ac的值；
（3）如图2，直线y=kx+m交抛物线P、Q两点，P在点A左边，Q在点B右边，PM⊥x轴于M，QN⊥x轴于N，AR⊥x轴交直线PQ于R，连RM、QB．直线y=kx+m交x轴正半轴于H点，若S_△RMA=4S_△QBN，求$\frac{BH}{MH}$的值．