11．下列计算正确的是（　　）

A．

$\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$

B．

$\sqrt{2}$×$\sqrt{8}$=4

C．

$\sqrt{6}$÷$\sqrt{5}$=$\frac{\sqrt{6}}{5}$

D．

$\sqrt{（-3）^{2}}$=-3

10．在购买某场足球赛门票时，设购买门票张数为x（张），现有两种购买方案：
方案一：若单位赞助广告费10000元，则该单位所购门票的价格为每张60元；（总费用=广告赞助费+门票费）
方案二：购买门票数不超过100张时，每张100元，若超过100元时，超过部分每张80元，
解答下列问题：
（1）方案一种，总费用为10000+60x．方案二中，当0≤x＜100时，总费用为100x；当x＞100时，总费用为80x+2000．
（2）如果购买本场足球赛门票超过100张，你将选择哪种方案，使总费用最省？请说明理由；
（3）甲，乙两单位分别采用方案一、方案二购买本场足球赛门票共700张，花去总费用计58000元，求甲，乙两单位各购买门票多少张？

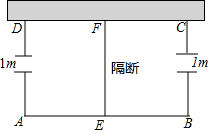9．如图所示，利用一面墙（墙的长度足够），用篱笆围成一个形如矩形ABCD的场地，在AD，BC边上各有一个宽为1m的缺口，在场地中有用篱笆做的隔断EF，且EF⊥AB，AB＞EF，已知所用篱笆总长度为38m．
（1）设隔断EF的长为x（m），请用含x的代数式表示AB的长．
（2）所围成形如矩形ABCD的场地的面积为100m²时，求AB的长．
（3）所围成矩形ABCD场地的面积能否为140m²？若能，求AB的长；若不能，说明理由．并写出所围成的矩形ABCD场地面积的最大值．

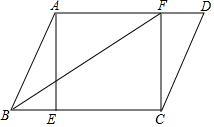8．如图，在平行四边形ABCD中，过点A作AE⊥BC交BC边于点E，点F在边AD上，且DF=BE．
（1）求证：四边形AECF是矩形．
（2）若BF平分∠ABC，且DF=1，AF=3，求线段BF的长．

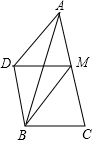7．如图在△ABC中，∠BAC=30°，AB=AC=6，M为AC边上一动点（不与A，C重合），以MA、MB为一组邻边作平行四边形MADB，则平行四边形MADB的对角线MD的最小值是3．

6．已知，如图，AB与CD交于点O．
（1）如图1，若AC∥BD，求证：∠A+∠C=∠B+∠D；
（2）如图2，若AC不平行BD，（1）中的结论是否仍然成立？请判断并证明你的结论．

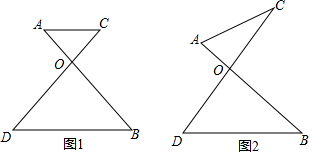
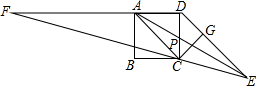5．如图，四边形ABCD是正方形，DE∥AC，CE=AC，EC的延长线DA的延长线交于F，连AE交CD于P，作CG⊥DE于G，则下列结论：①AE平分∠CED；②S_△ADP=S_△EPC；③∠F=∠EAC；④CE=2CG．其中正确的说法有（　　）

A．

1

B．

2

C．

3

D．

4

4．小兰在玩具工厂劳动，做4个小狗，7个小汽车用去3小时42分，做5个小狗，6个小汽车用去3小时37分，平均做1个小狗与1个小汽车各用多少时间？通过计算得知平均做1个狗和做1个汽车用的时间分别是17和22分钟．

3．如图，直线c截两平行直线a，b，则下列式子中一定成立的是（　　）

A．

∠1=∠5

B．

∠1=∠4

C．

∠2=∠3

D．

∠1=∠2

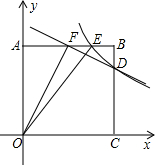2．如图，正方形AOCB的边长为4，反比例函数的图象过点E（3，4），与线段BC交于点D，直线y=-$\frac{1}{2}$x+b过点D，与线段AB相交于点F．
（1）求点F的坐标；
（2）连接OF、OE，探究∠AOF与∠EOC的数量关系，并证明；
（3）在x轴上找两点M，N，使MN=2，且使四边形AMND周长最小，求M，N两点的坐标．