
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,在△ABC中,∠B=25°,∠C=30°.
如图,在△ABC中,∠B=25°,∠C=30°.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题

查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 同角或等角的余角相等 | |
| B. | 三角形的三个内角和为180° | |
| C. | 平行于同一直线的两条直线平行 | |
| D. | 等腰三角形的高、中线、角平分线都重合 |
查看答案和解析>>
科目: 来源: 题型:解答题
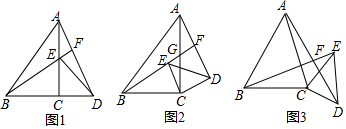
查看答案和解析>>
科目: 来源: 题型:解答题
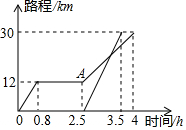 周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时候达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时候达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:查看答案和解析>>
科目: 来源: 题型:解答题
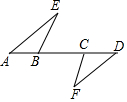 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由.查看答案和解析>>
科目: 来源: 题型:解答题
| 羽毛球数n | 100 | 200 | 300 | 400 | 500 | 600 | 1000 | 2000 |
| 优等品数m | 85 | 184 | 261 | 366 | 450 | 552 | 893 | 1804 |
| 优等品率$\frac{m}{n}$ | 0.85 | 0.92 | 0.87 | 0.915 | a | 0.92 | 0.893 | 0.902 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com