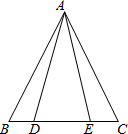9．阅读并填空：如图，已知在△ABC中，AB=AC，点D、E在边BC上，且AD=AE，试说明BD=CE的理由．
解：因为AB=AC，
所以∠B=∠C（等边对等角）．
因为AD=AE，
所以∠AED=∠ADE（等边对等角）．
在△ABE与△ACD中，
∠B=∠C，
∠AED=∠ADE，
AB=AC
所以△ABE≌△ACD（AAS）
所以BE=CD（全等三角形对应边相等），
所以BD=CE（等式性质）．
即BD=CE．

8．如果关于x的分式方程$\frac{ax}{x-1}$+$\frac{1}{x+2}$=0有增根，那么增根可能是（　　）

A．

x=1

B．

x=-2

C．

x=1或x=-2

D．

无法确定

7．下列计算错误的是（　　）

A．

$\frac{{x}^{3}{y}^{2}}{{x}^{2}{y}^{3}}$=$\frac{x}{y}$

B．

$\frac{a-1}{b-1}$=$\frac{a}{b}$

C．

$\frac{a-b}{b-a}$=-1

D．

$\frac{1}{c}$+$\frac{2}{c}$=$\frac{3}{c}$

6．海中有A、B、C三个小岛，A岛在B岛正西方距离400海里处（如图所示），C岛在B岛的北偏东37°方向500海里处．

（1）用1厘米代表200海里，请根据题意在图中画出C岛的位置；量出图中AC的长度为4厘米．（四舍五入到整厘米数）；那么A、C两地的实际距离约为800海里．
（2）甲、乙两货轮同时从A岛出发，甲沿A-C-B方向，乙沿A-B-C方向，10小时相遇，此时甲货轮比乙货轮多行驶了100海里，求甲乙两货轮的速度．
（3）若B岛需要大米和玉米共30吨，C岛需要大米和玉米共50吨，现从A岛运输20吨大米与60吨玉米到B岛和C岛，运输费用共为10600元（每吨的运输费用如下表所示）那么运到B岛的大米与玉米各是多少吨？：

	到B岛的运费（元/吨）	到C岛的运费（元/吨）
大米	100	200
玉米	80	150

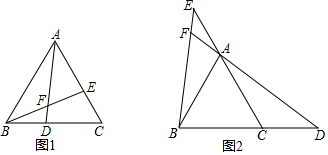5．已知等边△ABC中，D，E分别是边BC，AC所在直线上的两点，且BD=CE，直线AD，BE交于点F．
（1）把下面的解答过程补充完整，并在括号内注明理由．
当点D，E分别在线段BC，AC上时（如图1）
①求证：AD=BE；②求∠AFE的度数；
①证明：∵△ABC是等边三角形（已知）
∴AB=AC（等边三角形的三条边都相等）
∠ABD=∠BCE（等边三角形的三个角都是60°）
∵BD=CE（已知）
∴△ABD≌△BCE（SAS）
∴AD=BE（全等三角形的对应边相等）
②解：由①得∠BAD=∠CBE（全等三角形的对应边相等）
∵∠AFB+∠BAD+∠ABF=180°（三角形的内角和等于180°）
∴∠AFB+∠CBE+∠ABF=180°（等量代换）
∵∠CBE+∠ABF=∠ABC=60°（等边三角形的三个角都是60°）
∴∠AFB=120°（等式的性质）
∵∠AFE+∠AFB=180°（平角的定义）
∴∠AFE=60°．
（2）当点D在线段BC的延长线上，点E在线段CA的延长线上时，如图2，
①求证：AD=BE；
②求∠AFE的度数．

4．某景区的旅游线路如图1所示，其中A为入口，B，C，D为风景点，甲游客以一定的速度沿路线“A→B→C→D→A”步行游览，在每个景点他都逗留一段时间，当他回到A处时，共用去4.5h，甲步行的路程s（km）与游览时间t（h）之间的部分函数图象如图2所示．根据图回答下列问题：

（1）图2中自变量是t，因变量是s．
（2）改游客在景点B处逗留的时间是1.2小时，他从景点B到景点C时行走的平均速度是2千米/时．
（3）该游客沿路线“A→B→C→D→A”共步行的路程是3.5km．
（4）图2中点P表示该游客游览3.4小时后步行2.6km．

3．先化简，再求值：（$\frac{1}{x-2}$+$\frac{1}{x+2}$）÷$\frac{{x}^{2}}{{x}^{2}-4}$，其中x=$\sqrt{2}$．

2．泉州市某校准备组织教师、学生、家长到福州进行参观学习活动，旅行社代办购买动车票，动车票价格如表所示：

运行区间		大人票价		学生票价
出发站	终点站	一等座	二等座	一等座	二等座
泉州	福州	65（元）	54（元）	65（元）	40（元）

根据报名总人数，若所有人员都买一等座的动车票，则共需13650元；若都买二等座动车票，则共需8820元．已知家长人数是教师人数的2倍．
（1）设参加活动的老师有m人，请直接用含m的代数式表示：教师和家长都购买一等动车票所需的总费用；
（2）求参加活动的教师、家长、学生各有多少人？
（3）如果二等座动车票共买到x张，其中学生全部购买二等座动车票，剩余的人员买一等座动车票，且买票的总费用不低于9000元，求x的最大值．

1．如图，射线ON、OE、OS、OW分别表示从点O出发北、东、南、西四个方向，点A在点O的北偏东45°方向，点B在点O的北偏西30°方向．
（1）画出射线OB，若∠BOC与∠AOB互余，请在图1或备用图中画出∠BOC；
（2）若OP是∠AOC的角平分线，直接写出∠AOP的度数（不需要计算过程）．

20．如图，在梯形ABCD中，AB∥CD，AD=BC=4，CD=2，AB=6，DM⊥AB，垂足为M，CN⊥AB，垂足为N，点P、Q分别是线段DM、CN上的动点，且DP=NQ，顺次联结AP、PQ、QB，设DP=t．
（1）求PQ的长（用含t的代数式表示）；
（2）如果四边形APQB是等腰梯形，求t的值；
（3）联结PN，当△PNQ时等腰三角形时，求t的值．