
科目: 来源: 题型:解答题
 如图1,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、CA的延长线于点E、F.
如图1,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、CA的延长线于点E、F.查看答案和解析>>
科目: 来源: 题型:解答题
 在某节习题课上.老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.
在某节习题课上.老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E,F为线段BC上的两点,且CE=BF,连接AF,过点C作CD⊥AF于点G,交AB于点D,连接DE,交AF于点M.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E,F为线段BC上的两点,且CE=BF,连接AF,过点C作CD⊥AF于点G,交AB于点D,连接DE,交AF于点M.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,在平面直角坐标系中,O为坐标原点,△AOB为等边三角形,点A的坐标是(4$\sqrt{3}$,0),点B在第一象限,AC是∠OAB的平分线,并且与y轴交于点E,点M为直线AC上一个动点,把△AOM绕点A顺时针旋转,使边AO与边B重合,得到△ABD.假设反比例函数y=$\frac{k}{x}$(x>0)图象经过点B
如图,在平面直角坐标系中,O为坐标原点,△AOB为等边三角形,点A的坐标是(4$\sqrt{3}$,0),点B在第一象限,AC是∠OAB的平分线,并且与y轴交于点E,点M为直线AC上一个动点,把△AOM绕点A顺时针旋转,使边AO与边B重合,得到△ABD.假设反比例函数y=$\frac{k}{x}$(x>0)图象经过点B查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
 AB,CD是⊙O的两条弦,若OE⊥AB于点E,OF⊥CD于点F,且$\widehat{AB}$=$\widehat{CD}$,求证:OE=OF.
AB,CD是⊙O的两条弦,若OE⊥AB于点E,OF⊥CD于点F,且$\widehat{AB}$=$\widehat{CD}$,求证:OE=OF.查看答案和解析>>
科目: 来源: 题型:解答题
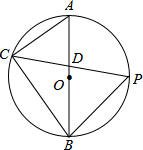 如图,AB是⊙O的直径,点P是$\widehat{AB}$的中点.
如图,AB是⊙O的直径,点P是$\widehat{AB}$的中点.查看答案和解析>>
科目: 来源: 题型:解答题
 小明与小颖玩一个投镖游戏,投镖所用的靶子如图,规定小明,规定小明投中黑色区域得2分,投中灰色区域减1分,投中白色区域不得分;小颖投中黑色区域减1分,投中灰色区域得2分,投中白色区域不得分.假设两人投镖均属随意性的,那么谁获胜的可能性大?请说明理由.
小明与小颖玩一个投镖游戏,投镖所用的靶子如图,规定小明,规定小明投中黑色区域得2分,投中灰色区域减1分,投中白色区域不得分;小颖投中黑色区域减1分,投中灰色区域得2分,投中白色区域不得分.假设两人投镖均属随意性的,那么谁获胜的可能性大?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com