11．问题情境：如图1，在?ABCD中，E、F、G、H分别为AB、BC、CD、DA边上的动点，连接EG、HF，相较于点O，切∠HOE=∠ADC，若AB=a，AD=b，试探究：EG与FH的数量关系，小聪建议分以下三步进行，请你解答：
（1）特殊情况，探索结论
当?ABCD是边长为a的正方形（如图2），请写出EG盒FH的数量关系（不必证明）；
（2）尝试变题，再探思路
当?ABCD是边长为a的菱形时（如图3）EG与FH又有怎样的数量关系呢？
小聪展示出如下正确的解法（不完整）
如图3，分别过点G、H、作GM⊥AB于点M，HN⊥⊥BC于点N，则∠GME=∠HNF=90°
∵AB×GM=BC×HN，AB=BC
∴GM=HN
…
请补全小聪的解答过程
（3）特例启发，解答题目
猜想：图1中EG与FH的数量关系是$\frac{EG}{FH}=\frac{b}{a}$，并说明理由．

10．我们知道，任何一个三角形的三条内角平分线相交于一点．如图，若△ABC的三条内角平分线相交于点I，过I作DE⊥AI分别交AB、AC于点D、E．
（1）请你通过计算，填写表格．
（2）从表中你发现了∠BIC与∠BDI之间有何数量关系，请写出来，并说明其中的道理，它们的关系是∠BIC=∠BDI．

∠BAC的度数	60°	100°
∠BIC的度数	120°	140°
∠BDI的度数	120°	140°

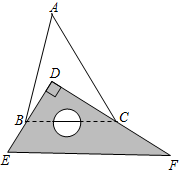9．已知将一块直角三角板DEF放置在△ABC上，使得该三角板的两条直角边DE，D、F恰好分别经过点B、C．
（1）∠DBC+∠DCB=90度；
（2）试说明：∠ABD+∠ACD=90°-∠A．

8．客运站售票大厅为方便旅客购票，同时又节约成本，常根据客流量决定开放售票窗口数，假定每个窗口平均每小时可以售出30张，开放4个售票窗口时，需要5h才能使当天购票的旅客全部买到票．
（1）当天一共售出多少张票？
（2）设开放x个售票窗口时，需要yh才能使当天购票的旅客全部买到票，试求出y与x之间的函数关系式；
（3）如果准备在4h内是当天购票的旅客全部买到票，那么至少开放几个售票窗口．
（4）已知客运站售票大厅最多可以同时开放8个售票窗口，那么最少多少时可以使当天购票的旅客全部买到票．

7．下列计算正确的是（　　）

	A．	（a-$\frac{1}{2}$b）2=a2-$\frac{1}{2}$ab+$\frac{1}{4}$b2		B．	-2a2（$\frac{1}{2}$ab+b2）=-a3b+b2a2
	C．	-$\frac{1}{2}$a2bn•（3anbn+1）=-$\frac{3}{2}$a2nb${\;}^{{n}^{2}+n}$		D．	（a-b）（-a-2b）=-a2-ab+2b2

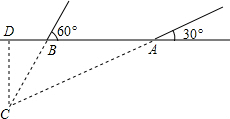6．2014年3月，某海域发生航班失联事件，我海事救援部门用高频海洋探测仪进行海上搜救，分别在A、B两个探测点探测到C处是信号发射点，已知A、B两点相距400m，探测线与海平面的夹角分别是30°和60°，若CD的长是点C到海平面的最短距离．
（1）问BD与AB有什么数量关系，试说明理由；
（2）求信号发射点的深度．（结果精确到1m，参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）

5．如图是一个餐盘，它的外围是由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成，已知正三角形的边长为10，则该餐盘的面积是（　　）

A．

50π-50$\sqrt{3}$

B．

50π-25$\sqrt{3}$

C．

25π+50$\sqrt{3}$

D．

50π

4．如图所示，半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动．且滚动至扇形O′A′B′处，则顶点O所经过的路线总长是$\frac{4}{3}$π．

3．抛物线y=x²-2x与坐标轴的交点个数为（　　）

A．

0个

B．

1个

C．

2个

D．

3个

2．如图，直角坐标系中，点P（t，0）是x轴正半轴上的一个动点，过点P作y轴的平行线，分别与直线$y=\frac{2}{3}x$，直线y=-x交于A，B两点，以AB为边向右侧作正方形ABCD．
当点（3，0）在正方形ABCD内部时，t的取值范围是$\frac{9}{8}$＜t＜3．