
科目: 来源: 题型:解答题
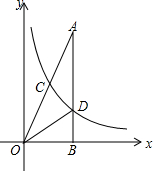 如图,在Rt△AOB中∠ABO=90°,点B在x轴上,点C(1,m)为OA的中点,一反比例函数的图象经过点C,交AB于点D.
如图,在Rt△AOB中∠ABO=90°,点B在x轴上,点C(1,m)为OA的中点,一反比例函数的图象经过点C,交AB于点D.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
 【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).
【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).查看答案和解析>>
科目: 来源: 题型:填空题
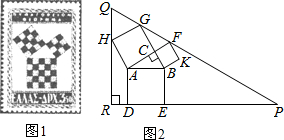 勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票图1所示.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图2的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边PQ上,则RQ=7+2$\sqrt{3}$,△PQR的周长等于27+13$\sqrt{3}$.
勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票图1所示.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图2的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边PQ上,则RQ=7+2$\sqrt{3}$,△PQR的周长等于27+13$\sqrt{3}$.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点(A在B点左侧),与y轴交于点C,对称轴为直线x=$\frac{1}{2}$,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限);
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点(A在B点左侧),与y轴交于点C,对称轴为直线x=$\frac{1}{2}$,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限);查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
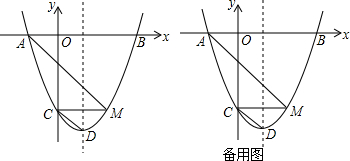
 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com