10．下列命题：①对角线相等的四边形是矩形；②正多边形都是轴对称图形；③通过对足球迷健康状况的调查可以了解我国公民的健康状况；④球的主视图、左视、俯视图都是圆；⑤如果一个角的两边与另一个解的两边分别平行，那么这两个角相等，其中是真命题的有②④（只需填写序号）．

9．计算：$\sqrt{27}$-$\frac{1}{2-\sqrt{3}}$-$\sqrt{12}$=-2．

8．某校学生来自甲、乙、丙三个地区，其人数比为2：3：5，如图所示的扇形统计图表上述分布情况．已知来自甲地区的为160人，则下列说法不正确的是（　　）

	A．	扇形甲的圆心角是72°
	B．	学生的总人数是800人
	C．	丙地区的人数比乙地区的人数多160人
	D．	甲地区的人数比丙地区的人数少160人

7．如图，CD为⊙O的直径，点B在⊙O上，连接BC、BD，过点B的切线AE与CD的延长线交于点A，OE∥BD，交BC于点F，交AE于点E．
（1）求证：∠E=∠C；
（2）当⊙O的半径为3，tanC=$\frac{2}{5}$时，求BE的长．

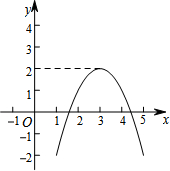6．对某一个函数给出如下定义：如果存在实数M，对于任意的函数值y，都满足y≤M，那么称这个函数是有上界函数，在所有满足条件的M中，其最小值称为这个函数的上确界．例如，图中的函数是有上界函数，其上确界是2．
（1）分别判断函数y=-$\frac{1}{x}$（x＜0）和y=2x-3（x＜2）是不是有上界函数？如果是有上界函数，求其上确界；
（2）如果函数y=-x+2（a≤x≤b，b＞a）的上确界是b，且这个函数的最小值不超过2a+1，求a的取值范围；
（3）如果函数y=x²-2ax+2（1≤x≤5）是以3为上确界的有上界函数，求实数a的值．

5．在平面直角坐标系xOy中，抛物线y=ax²+bx+1经过A（1，3），B（2，1）两点．
（1）求抛物线及直线AB的解析式；
（2）点C在抛物线上，且点C的横坐标为3．将抛物线在 点A，C之间的部分（包含点A，C）记为图象G，如果图象G沿y轴向上平移t（t＞0）个单位后与直线  AB只有一个公共点，求t的取值范围．

4．如图，AB是⊙O的直径，以AB为边作△ABC，使得AC=AB，BC交⊙O于点D，联结OD，过点D作⊙O的切线，交AB延长线于点E，交AC于点F．
（1）求证：OD∥AC；
（2）当AB=10，cos∠ABC=$\frac{\sqrt{5}}{5}$时，求BE的长．

3．某校九年级有200名学生参加《中小学生国家体质健康标准》测试赛活动．为了解本次测试的成绩分布情况，从中抽取了20名学生的成绩进行分组整理．现已完成前15个数据的整理，还有后5个数据尚未累计：
62，83，76，87，70，
学生测试成绩频数分布表                           

成绩x（分）	频数累计	频数	频率
50≤x＜60		3	0.15
60≤x＜70	▁	2	0.10
70≤x＜80		4	0.20
80≤x＜90		6	0.30
90≤x≤100	正	5	0.25
合计		20	1.00

（1）请将剩余的5个数据累计在“学生测试成绩频数分布表”中，填上各组的频数与频率，并补全“学生测试成绩频数分布直方图”；
（2）这20个数据的中位数所在组的成绩范围是80≤x＜90；
（3）请估计这次该校九年级参加测试赛的学生中约有多少学生成绩不低于80分．

2．如图，在△ABC中，D为AB边上一点，DE∥BC交AC于点E，如果$\frac{AD}{DB}$=$\frac{3}{5}$，AE=6，那么EC的长为10．

1．如图，二次函数y=$\frac{4}{3}$x²+bx+c的图象与x轴交于A（3，0），B（-1，0），与y轴交于点C．若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动．
（1）求该二次函数的解析式及点C的坐标；
（2）当点P运动到B点时，点Q停止运动，这时，在x轴上是否存在点E，使得以A，E，Q为顶点的三角形为等腰三角形？若存在，请求出E点坐标；若不存在，请说明理由．
（3）当P，Q运动到t秒时，△APQ沿PQ翻折，点A恰好落在抛物线上D点处，请判定此时四边形APDQ的形状，并求出D点坐标．
（4）在AC段的抛物线上有一点R，过点R作平行于y轴的直线交AC于M，当线段RM的长为最大时，请直接写出点R的坐标．