
科目: 来源: 题型:填空题
 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①BG⊥DE;②$\frac{DG}{GC}=\frac{GO}{CE}$;③△BCG∽△EFO;④${(a-b)^2}•{S_{△EFO}}={b^2}•{S_{△DGO}}$.其中正确结论的序号是①③④.(把所有正确结论的序号都填在横线上)
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O.设AB=a,CG=b(a>b).下列结论:①BG⊥DE;②$\frac{DG}{GC}=\frac{GO}{CE}$;③△BCG∽△EFO;④${(a-b)^2}•{S_{△EFO}}={b^2}•{S_{△DGO}}$.其中正确结论的序号是①③④.(把所有正确结论的序号都填在横线上)查看答案和解析>>
科目: 来源: 题型:解答题
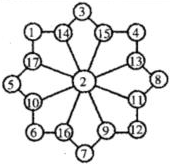 如图,在17个小圆圈里分别填写着1至17这些自然数,每个小四边形上的4个数字之和都是34.想想看,如何调整一下这些数,使每个小四边形上的数字之和变为38?
如图,在17个小圆圈里分别填写着1至17这些自然数,每个小四边形上的4个数字之和都是34.想想看,如何调整一下这些数,使每个小四边形上的数字之和变为38?查看答案和解析>>
科目: 来源: 题型:解答题
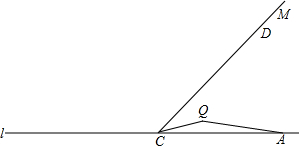
查看答案和解析>>
科目: 来源: 题型:解答题
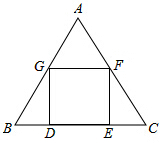 △ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
△ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2}{3π}$,求图中阴影部分的面积.
如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2}{3π}$,求图中阴影部分的面积.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
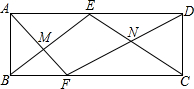 如图,矩形ABCD中,点E、F分别在边AD、BC上,AF、BE交于M,DF、CE交于N,且△AME的面积是4,△BMF的面积是2,△DCN的面积是3.则矩形EMFN的面积是2$\sqrt{2}$+3.
如图,矩形ABCD中,点E、F分别在边AD、BC上,AF、BE交于M,DF、CE交于N,且△AME的面积是4,△BMF的面积是2,△DCN的面积是3.则矩形EMFN的面积是2$\sqrt{2}$+3.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com