
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
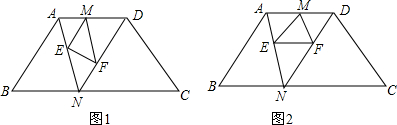
 如图,正方形OEFG绕着边长为30的正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.
如图,正方形OEFG绕着边长为30的正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.查看答案和解析>>
科目: 来源: 题型:解答题
 如图所示,以定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上(AM>MD).
如图所示,以定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上(AM>MD).查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
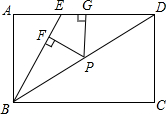 如图,E是矩形ABCD边AD上的一点,且BE=ED,P是对角线BD上任意一点,PF⊥BE于F,PG⊥AD与G,请你猜想PF、PG、AB它们之间有什么关系?并证明你的结论.
如图,E是矩形ABCD边AD上的一点,且BE=ED,P是对角线BD上任意一点,PF⊥BE于F,PG⊥AD与G,请你猜想PF、PG、AB它们之间有什么关系?并证明你的结论.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,∠AGF=∠ABC,∠1+∠2=180°.
如图,∠AGF=∠ABC,∠1+∠2=180°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com