
科目: 来源: 题型:选择题
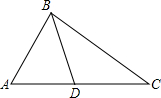 如图,下列条件不能判定△ADB∽△ABC的是( )
如图,下列条件不能判定△ADB∽△ABC的是( )| A. | ∠ABD=∠ACB | B. | ∠ADB=∠ABC | C. | AB2=AD•AC | D. | $\frac{AD}{AB}$=$\frac{AB}{BC}$ |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | -1≤m<0 | B. | -1<m≤0 | C. | -1≤m≤0 | D. | -1<m<0 |
查看答案和解析>>
科目: 来源: 题型:选择题
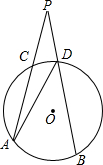 如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知$\widehat{AB}$和$\widehat{CD}$所对的圆心角分别为90°和50°,则∠P=( )
如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知$\widehat{AB}$和$\widehat{CD}$所对的圆心角分别为90°和50°,则∠P=( )| A. | 45° | B. | 40° | C. | 25° | D. | 20° |
查看答案和解析>>
科目: 来源: 题型:选择题
 一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 10:00 | B. | 12:00 | C. | 13:00 | D. | 16:00 |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 这组数据的众数是170 | |
| B. | 这组数据的中位数是169 | |
| C. | 这组数据的平均数是169 | |
| D. | 若从8名学生中任选1名学生参加校文艺会演,则这名学生的身高不低于170的概率为$\frac{1}{2}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
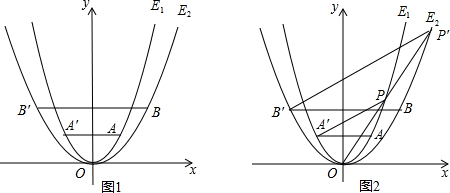
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com