
科目: 来源: 题型:解答题
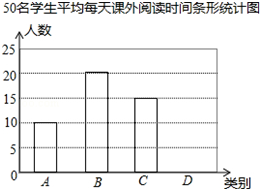 课外阅读是提高学生素养的重要途径.某校为了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间t(小时).根据t的长短分为A,B,C,D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:
课外阅读是提高学生素养的重要途径.某校为了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间t(小时).根据t的长短分为A,B,C,D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:| 类别 | 时间t(小时) | 人数 |
| A | t<0.5 | 10 |
| B | 0.5≤t<1 | 20 |
| C | 1≤t<1.5 | 15 |
| D | t≥1.5 | a |
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
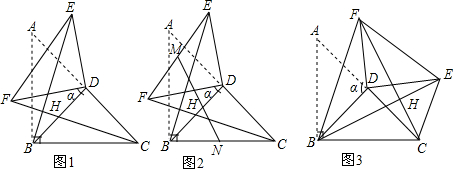
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=x+1和x轴上,则点B1的坐标是(1,1);点Bn的坐标是${B_n}({{2^n}-1,{2^{n-1}}})$.(用含n的代数式表示)
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=x+1和x轴上,则点B1的坐标是(1,1);点Bn的坐标是${B_n}({{2^n}-1,{2^{n-1}}})$.(用含n的代数式表示)查看答案和解析>>
科目: 来源: 题型:解答题
 已知在平面直角坐标系xOy中(如图),抛物线y=ax2-4与x轴的负半轴相交于点A,与y轴相交于点B,AB=2$\sqrt{5}$,点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D,设点P的横坐标为m.
已知在平面直角坐标系xOy中(如图),抛物线y=ax2-4与x轴的负半轴相交于点A,与y轴相交于点B,AB=2$\sqrt{5}$,点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D,设点P的横坐标为m.查看答案和解析>>
科目: 来源: 题型:解答题
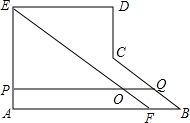 如图,在多边形ABCDE中,∠A=∠AED=∠D=90°,AB=5,AE=2,ED=3,过点E作EF∥CB交AB于点F,FB=1,过AE上的点P作PQ∥AB交线段EF于点O,交折线BCD于点Q,设AP=x,PO•OQ=y.
如图,在多边形ABCDE中,∠A=∠AED=∠D=90°,AB=5,AE=2,ED=3,过点E作EF∥CB交AB于点F,FB=1,过AE上的点P作PQ∥AB交线段EF于点O,交折线BCD于点Q,设AP=x,PO•OQ=y.查看答案和解析>>
科目: 来源: 题型:解答题
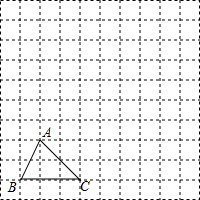 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(项点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(项点是网格线的交点).查看答案和解析>>
科目: 来源: 题型:填空题
 如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请用无刻度直尺在线段AB上画出点P,使AP=$\frac{2\sqrt{17}}{3}$,并保留作图痕迹.(备注:本题只是找点不是证明,∴只需连接一对角线就行)
如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请用无刻度直尺在线段AB上画出点P,使AP=$\frac{2\sqrt{17}}{3}$,并保留作图痕迹.(备注:本题只是找点不是证明,∴只需连接一对角线就行)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com